dsdTree.c File Reference

#include "dsdInt.h"
#include "misc/util/utilTruth.h"
#include "opt/dau/dau.h"

Include dependency graph for dsdTree.c:

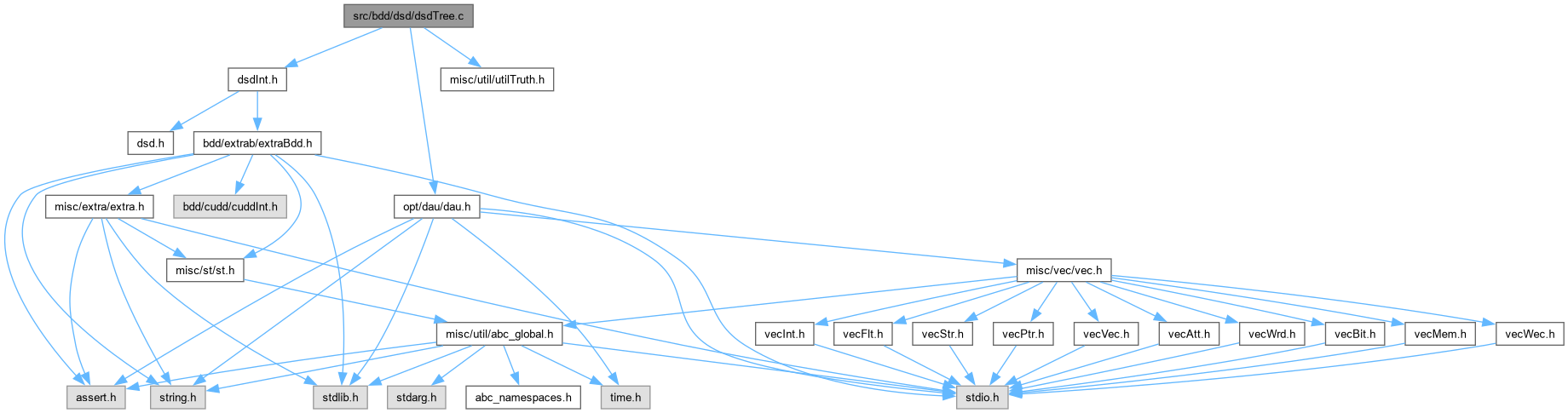
Go to the source code of this file.

Functions
Dsd_Node_t *	Dsd_TreeNodeCreate (int Type, int nDecs, int BlockNum)
	FUNCTION DEFINITIONS ///.
void	Dsd_TreeNodeDelete (DdManager *dd, Dsd_Node_t *pNode)
void	Dsd_TreeUnmark (Dsd_Manager_t *pDsdMan)
void	Dsd_TreeNodeGetInfo (Dsd_Manager_t *pDsdMan, int *DepthMax, int *GateSizeMax)
void	Dsd_TreeNodeGetInfoOne (Dsd_Node_t *pNode, int *DepthMax, int *GateSizeMax)
int	Dsd_TreeGetAigCost_rec (Dsd_Node_t *pNode)
int	Dsd_TreeGetAigCost (Dsd_Node_t *pNode)
int	Dsd_TreeCountNonTerminalNodes (Dsd_Manager_t *pDsdMan)
int	Dsd_TreeCountNonTerminalNodesOne (Dsd_Node_t *pRoot)
int	Dsd_TreeCountPrimeNodes (Dsd_Manager_t *pDsdMan)
int	Dsd_TreeCountPrimeNodesOne (Dsd_Node_t *pRoot)
int	Dsd_TreeCollectDecomposableVars (Dsd_Manager_t *pDsdMan, int *pVars)
Dsd_Node_t **	Dsd_TreeCollectNodesDfs (Dsd_Manager_t *pDsdMan, int *pnNodes)
Dsd_Node_t **	Dsd_TreeCollectNodesDfsOne (Dsd_Manager_t *pDsdMan, Dsd_Node_t *pNode, int *pnNodes)
int	Dsd_TreeNonDsdMax_rec (Dsd_Node_t *pNode)
int	Dsd_TreeNonDsdMax (Dsd_Manager_t *pDsdMan, int Output)
int	Dsd_TreeSuppSize_rec (Dsd_Node_t *pNode)
int	Dsd_TreeSuppSize (Dsd_Manager_t *pDsdMan, int Output)
void	Dsd_TreePrint3_rec (Vec_Str_t *p, Dsd_Node_t *pNode)
void	Dsd_TreePrint3 (void *pStr, Dsd_Manager_t *pDsdMan, int Output)
void	Dsd_TreePrint4_rec (Vec_Str_t *p, Dsd_Node_t *pNode)
void	Dsd_TreePrint4 (void *pStr, Dsd_Manager_t *pDsdMan, int Output)
void	Dsd_TreePrint (FILE *pFile, Dsd_Manager_t *pDsdMan, char *pInputNames[], char *pOutputNames[], int fShortNames, int Output, int OffSet)
word	Dsd_TreeFunc2Truth_rec (DdManager *dd, DdNode *bFunc)
void	Dsd_TreePrint2_rec (FILE *pFile, DdManager *dd, Dsd_Node_t *pNode, int fComp, char *pInputNames[])
void	Dsd_TreePrint2 (FILE *pFile, Dsd_Manager_t *pDsdMan, char *pInputNames[], char *pOutputNames[], int Output)
void	Dsd_NodePrint (FILE *pFile, Dsd_Node_t *pNode)
DdNode *	Dsd_TreeGetPrimeFunctionOld (DdManager *dd, Dsd_Node_t *pNode, int fRemap)

Function Documentation

Dsd_NodePrint()

void Dsd_NodePrint	(	FILE *	pFile,
		Dsd_Node_t *	pNode )

Function*************************************************************

Synopsis [Prints the decompostion tree into file.]

Description []

SideEffects []

SeeAlso []

Definition at line 1138 of file dsdTree.c.

{
    Dsd_Node_t * pNodeR;
    int SigCounter = 1;
    pNodeR = Dsd_Regular(pNode);
    Dsd_NodePrint_rec( pFile, pNodeR, pNodeR != pNode, "F", 0, &SigCounter );
}

Dsd_TreeCollectDecomposableVars()

int Dsd_TreeCollectDecomposableVars	(	Dsd_Manager_t *	pDsdMan,
		int *	pVars )

Function*************************************************************

Synopsis [Collects the decomposable vars on the PI side.]

Description []

SideEffects []

SeeAlso []

Definition at line 470 of file dsdTree.c.

{
    int nVars;
 
    // set the vars collected to 0
    nVars = 0;
    Dsd_TreeCollectDecomposableVars_rec( pDsdMan->dd, Dsd_Regular(pDsdMan->pRoots[0]), pVars, &nVars );
    // return the number of collected vars
    return nVars;
}

Dsd_TreeCollectNodesDfs()

Dsd_Node_t ** Dsd_TreeCollectNodesDfs	(	Dsd_Manager_t *	pDsdMan,
		int *	pnNodes )

Function*************************************************************

Synopsis [Creates the DFS ordered array of DSD nodes in the tree.]

Description [The collected nodes do not include the terminal nodes and the constant 1 node. The array of nodes is returned. The number of entries in the array is returned in the variale pnNodes.]

SideEffects []

SeeAlso []

Definition at line 555 of file dsdTree.c.

{
    Dsd_Node_t ** ppNodes;
    int nNodes, nNodesAlloc;
    int i;
 
    nNodesAlloc = Dsd_TreeCountNonTerminalNodes(pDsdMan);
    nNodes  = 0;
    ppNodes = ABC_ALLOC( Dsd_Node_t *, nNodesAlloc );
    for ( i = 0; i < pDsdMan->nRoots; i++ )
        Dsd_TreeCollectNodesDfs_rec( Dsd_Regular(pDsdMan->pRoots[i]), ppNodes, &nNodes );
    Dsd_TreeUnmark( pDsdMan );
    assert( nNodesAlloc == nNodes );
    *pnNodes = nNodes;
    return ppNodes;
}

Here is the call graph for this function:

Dsd_TreeCollectNodesDfsOne()

Dsd_Node_t ** Dsd_TreeCollectNodesDfsOne	(	Dsd_Manager_t *	pDsdMan,
		Dsd_Node_t *	pNode,
		int *	pnNodes )

Function*************************************************************

Synopsis [Creates the DFS ordered array of DSD nodes in the tree.]

Description [The collected nodes do not include the terminal nodes and the constant 1 node. The array of nodes is returned. The number of entries in the array is returned in the variale pnNodes.]

SideEffects []

SeeAlso []

Definition at line 585 of file dsdTree.c.

{
    Dsd_Node_t ** ppNodes;
    int nNodes, nNodesAlloc;
    nNodesAlloc = Dsd_TreeCountNonTerminalNodesOne(pNode);
    nNodes  = 0;
    ppNodes = ABC_ALLOC( Dsd_Node_t *, nNodesAlloc );
    Dsd_TreeCollectNodesDfs_rec( Dsd_Regular(pNode), ppNodes, &nNodes );
    Dsd_TreeUnmark_rec(Dsd_Regular(pNode));
    assert( nNodesAlloc == nNodes );
    *pnNodes = nNodes;
    return ppNodes;
}

Here is the call graph for this function:

Dsd_TreeCountNonTerminalNodes()

int Dsd_TreeCountNonTerminalNodes

(

Dsd_Manager_t *

pDsdMan

)

Function*************************************************************

Synopsis [Counts non-terminal nodes of the DSD tree.]

Description [Nonterminal nodes include all the nodes with the support more than 1. These are OR, EXOR, and PRIME nodes. They do not include the elementary variable nodes and the constant 1 node.]

SideEffects []

SeeAlso []

Definition at line 310 of file dsdTree.c.

{
    int Counter, i;
    Counter = 0;
    for ( i = 0; i < pDsdMan->nRoots; i++ )
        Counter += Dsd_TreeCountNonTerminalNodes_rec( Dsd_Regular( pDsdMan->pRoots[i] ) );
    Dsd_TreeUnmark( pDsdMan );
    return Counter;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreeCountNonTerminalNodesOne()

int Dsd_TreeCountNonTerminalNodesOne

(

Dsd_Node_t *

pRoot

)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 331 of file dsdTree.c.

{
    int Counter = 0;
 
    // go through the list of successors and call recursively 
    Counter = Dsd_TreeCountNonTerminalNodes_rec( Dsd_Regular(pRoot) );
 
    Dsd_TreeUnmark_rec( Dsd_Regular(pRoot) );
    return Counter;
}

Here is the caller graph for this function:

Dsd_TreeCountPrimeNodes()

int Dsd_TreeCountPrimeNodes

(

Dsd_Manager_t *

pDsdMan

)

Function*************************************************************

Synopsis [Counts prime nodes of the DSD tree.]

Description [Prime nodes are nodes with the support more than 2, that is not an OR or EXOR gate.]

SideEffects []

SeeAlso []

Definition at line 389 of file dsdTree.c.

{
    int Counter, i;
    Counter = 0;
    for ( i = 0; i < pDsdMan->nRoots; i++ )
        Counter += Dsd_TreeCountPrimeNodes_rec( Dsd_Regular( pDsdMan->pRoots[i] ) );
    Dsd_TreeUnmark( pDsdMan );
    return Counter;
}

Here is the call graph for this function:

Dsd_TreeCountPrimeNodesOne()

int Dsd_TreeCountPrimeNodesOne

(

Dsd_Node_t *

pRoot

)

Function*************************************************************

Synopsis [Counts prime nodes for one root.]

Description []

SideEffects []

SeeAlso []

Definition at line 410 of file dsdTree.c.

{
    int Counter = 0;
 
    // go through the list of successors and call recursively 
    Counter = Dsd_TreeCountPrimeNodes_rec( Dsd_Regular(pRoot) );
 
    Dsd_TreeUnmark_rec( Dsd_Regular(pRoot) );
    return Counter;
}

Here is the caller graph for this function:

Dsd_TreeFunc2Truth_rec()

word Dsd_TreeFunc2Truth_rec	(	DdManager *	dd,
		DdNode *	bFunc )

Function*************************************************************

Synopsis [Prints the decompostion tree into file.]

Description []

SideEffects []

SeeAlso []

Definition at line 1026 of file dsdTree.c.

{
    word Cof0, Cof1;
    int Level;
    if ( bFunc == b0 )
        return 0;
    if ( bFunc == b1 )
        return ~(word)0;
    if ( Cudd_IsComplement(bFunc) )
        return ~Dsd_TreeFunc2Truth_rec( dd, Cudd_Not(bFunc) );
    Level = dd->perm[bFunc->index];
    assert( Level >= 0 && Level < 6 );
    Cof0 = Dsd_TreeFunc2Truth_rec( dd, cuddE(bFunc) );
    Cof1 = Dsd_TreeFunc2Truth_rec( dd, cuddT(bFunc) );
    return (s_Truths6[Level] & Cof1) | (~s_Truths6[Level] & Cof0);
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreeGetAigCost()

int Dsd_TreeGetAigCost

(

Dsd_Node_t *

pNode

)

Function*************************************************************

Synopsis [Counts AIG nodes needed to implement this node.]

Description [Assumes that the only primes of the DSD tree are MUXes.]

SideEffects []

SeeAlso []

Definition at line 291 of file dsdTree.c.

{
    return Dsd_TreeGetAigCost_rec( Dsd_Regular(pNode) );
}

Here is the call graph for this function:

Dsd_TreeGetAigCost_rec()

int Dsd_TreeGetAigCost_rec

(

Dsd_Node_t *

pNode

)

Function*************************************************************

Synopsis [Counts AIG nodes needed to implement this node.]

Description []

SideEffects []

SeeAlso []

Definition at line 255 of file dsdTree.c.

{
    int i, Counter = 0;
 
    assert( pNode );
    assert( !Dsd_IsComplement( pNode ) );
    assert( pNode->nVisits >= 0 );
 
    if ( pNode->nDecs < 2 )
        return 0;
 
    // we don't want the two-input gates to count for non-decomposable blocks
    if ( pNode->Type == DSD_NODE_OR )
        Counter += pNode->nDecs - 1;
    else if ( pNode->Type == DSD_NODE_EXOR )
        Counter += 3*(pNode->nDecs - 1);
    else if ( pNode->Type == DSD_NODE_PRIME && pNode->nDecs == 3 )
        Counter += 3;
 
    // call recursively
    for ( i = 0; i < pNode->nDecs; i++ )
        Counter += Dsd_TreeGetAigCost_rec( Dsd_Regular(pNode->pDecs[i]) );
    return Counter;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreeGetPrimeFunctionOld()

DdNode * Dsd_TreeGetPrimeFunctionOld	(	DdManager *	dd,
		Dsd_Node_t *	pNode,
		int	fRemap )

Function*************************************************************

Synopsis [Retuns the function of one node of the decomposition tree.]

Description [This is the old procedure. It is now superceded by the procedure Dsd_TreeGetPrimeFunction() found in "dsdLocal.c".]

SideEffects []

SeeAlso []

Definition at line 1309 of file dsdTree.c.

{
    DdNode * bCof0,  * bCof1, * bCube0, * bCube1, * bNewFunc, * bTemp;
    int i;
    static int Permute[MAXINPUTS];
 
    assert( pNode );
    assert( !Dsd_IsComplement( pNode ) );
    assert( pNode->Type == DSD_NODE_PRIME );
 
    // transform the function of this block to depend on inputs
    // corresponding to the formal inputs
 
    // first, substitute those inputs that have some blocks associated with them
    // second, remap the inputs to the top of the manager (then, it is easy to output them)
 
    // start the function
    bNewFunc = pNode->G;  Cudd_Ref( bNewFunc );
    // go over all primary inputs
    for ( i = 0; i < pNode->nDecs; i++ )
    if ( pNode->pDecs[i]->Type != DSD_NODE_BUF ) // remap only if it is not the buffer
    {
        bCube0 = Extra_bddFindOneCube( dd, Cudd_Not(pNode->pDecs[i]->G) );  Cudd_Ref( bCube0 );
        bCof0 = Cudd_Cofactor( dd, bNewFunc, bCube0 );                     Cudd_Ref( bCof0 );
        Cudd_RecursiveDeref( dd, bCube0 );
 
        bCube1 = Extra_bddFindOneCube( dd,          pNode->pDecs[i]->G  );  Cudd_Ref( bCube1 );
        bCof1 = Cudd_Cofactor( dd, bNewFunc, bCube1 );                     Cudd_Ref( bCof1 );
        Cudd_RecursiveDeref( dd, bCube1 );
 
        Cudd_RecursiveDeref( dd, bNewFunc );
 
        // use the variable in the i-th level of the manager
//      bNewFunc = Cudd_bddIte( dd, dd->vars[dd->invperm[i]],bCof1,bCof0 );     Cudd_Ref( bNewFunc );
        // use the first variale in the support of the component
        bNewFunc = Cudd_bddIte( dd, dd->vars[pNode->pDecs[i]->S->index],bCof1,bCof0 );     Cudd_Ref( bNewFunc );
        Cudd_RecursiveDeref( dd, bCof0 );
        Cudd_RecursiveDeref( dd, bCof1 );
    }
 
    if ( fRemap )
    {
        // remap the function to the top of the manager
        // remap the function to the first variables of the manager
        for ( i = 0; i < pNode->nDecs; i++ )
    //      Permute[ pNode->pDecs[i]->S->index ] = dd->invperm[i];
            Permute[ pNode->pDecs[i]->S->index ] = i;
 
        bNewFunc = Cudd_bddPermute( dd, bTemp = bNewFunc, Permute );   Cudd_Ref( bNewFunc );
        Cudd_RecursiveDeref( dd, bTemp );
    }
 
    Cudd_Deref( bNewFunc );
    return bNewFunc;
}

Here is the call graph for this function:

Dsd_TreeNodeCreate()

Dsd_Node_t * Dsd_TreeNodeCreate	(	int	Type,
		int	nDecs,
		int	BlockNum )

FUNCTION DEFINITIONS ///.

Function*************************************************************

Synopsis [Create the DSD node.]

Description []

SideEffects []

SeeAlso []

Definition at line 61 of file dsdTree.c.

{
    // allocate memory for this node 
    Dsd_Node_t * p = (Dsd_Node_t *) ABC_ALLOC( char, sizeof(Dsd_Node_t) );
    memset( p, 0, sizeof(Dsd_Node_t) );
    p->Type       = (Dsd_Type_t)Type;       // the type of this block
    p->nDecs      = nDecs;                  // the number of decompositions
    if ( p->nDecs )
    {
        p->pDecs      = (Dsd_Node_t **) ABC_ALLOC( char, p->nDecs * sizeof(Dsd_Node_t *) );
        p->pDecs[0]   = NULL;
    }
    return p;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreeNodeDelete()

void Dsd_TreeNodeDelete	(	DdManager *	dd,
		Dsd_Node_t *	pNode )

Function*************************************************************

Synopsis [Frees the DSD node.]

Description []

SideEffects []

SeeAlso []

Definition at line 87 of file dsdTree.c.

{
    if ( pNode->G )  Cudd_RecursiveDeref( dd, pNode->G );
    if ( pNode->S )  Cudd_RecursiveDeref( dd, pNode->S );
    ABC_FREE( pNode->pDecs );
    ABC_FREE( pNode );
}

Here is the caller graph for this function:

Dsd_TreeNodeGetInfo()

void Dsd_TreeNodeGetInfo	(	Dsd_Manager_t *	pDsdMan,
		int *	DepthMax,
		int *	GateSizeMax )

Function*************************************************************

Synopsis [Getting information about the node.]

Description [This function computes the max depth and the max gate size of the tree rooted at the node.]

SideEffects []

SeeAlso []

Definition at line 156 of file dsdTree.c.

{
    int i;
    s_DepthMax    = 0;
    s_GateSizeMax = 0;
 
    for ( i = 0; i < pDsdMan->nRoots; i++ )
        Dsd_TreeGetInfo_rec( Dsd_Regular( pDsdMan->pRoots[i] ), 0 );
 
    if ( DepthMax ) 
        *DepthMax     = s_DepthMax;
    if ( GateSizeMax ) 
        *GateSizeMax  = s_GateSizeMax;
}

Dsd_TreeNodeGetInfoOne()

void Dsd_TreeNodeGetInfoOne	(	Dsd_Node_t *	pNode,
		int *	DepthMax,
		int *	GateSizeMax )

Function*************************************************************

Synopsis [Getting information about the node.]

Description [This function computes the max depth and the max gate size of the tree rooted at the node.]

SideEffects []

SeeAlso []

Definition at line 183 of file dsdTree.c.

{
    s_DepthMax    = 0;
    s_GateSizeMax = 0;
 
    Dsd_TreeGetInfo_rec( Dsd_Regular(pNode), 0 );
 
    if ( DepthMax ) 
        *DepthMax     = s_DepthMax;
    if ( GateSizeMax ) 
        *GateSizeMax  = s_GateSizeMax;
}

Here is the caller graph for this function:

Dsd_TreeNonDsdMax()

int Dsd_TreeNonDsdMax	(	Dsd_Manager_t *	pDsdMan,
		int	Output )

Definition at line 655 of file dsdTree.c.

{
    if ( Output == -1 ) 
    {
        int i, Res = 0;
        for ( i = 0; i < pDsdMan->nRoots; i++ )
            Res = Abc_MaxInt( Res, Dsd_TreeNonDsdMax_rec( Dsd_Regular( pDsdMan->pRoots[i] ) ) );
        return Res;
    }
    else 
    {
        assert( Output >= 0 && Output < pDsdMan->nRoots );
        return Dsd_TreeNonDsdMax_rec( Dsd_Regular( pDsdMan->pRoots[Output] ) );
    }
}

Here is the call graph for this function:

Dsd_TreeNonDsdMax_rec()

int Dsd_TreeNonDsdMax_rec

(

Dsd_Node_t *

pNode

)

Function*************************************************************

Synopsis [Returns the size of the largest non-DSD block.]

Description []

SideEffects []

SeeAlso []

Definition at line 641 of file dsdTree.c.

{
    if ( pNode->Type == DSD_NODE_CONST1 )
        return 0;
    if ( pNode->Type == DSD_NODE_BUF )
        return 0;
    int MaxBlock = pNode->Type == DSD_NODE_PRIME ? pNode->nDecs : 0;
    for ( int i = 0; i < pNode->nDecs; i++ )
    {
        int MaxThis = Dsd_TreeNonDsdMax_rec( Dsd_Regular( pNode->pDecs[i] ) );
        MaxBlock = Abc_MaxInt( MaxBlock, MaxThis );
    }
    return MaxBlock;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreePrint()

void Dsd_TreePrint	(	FILE *	pFile,
		Dsd_Manager_t *	pDsdMan,
		char *	pInputNames[],
		char *	pOutputNames[],
		int	fShortNames,
		int	Output,
		int	OffSet )

Function*************************************************************

Synopsis [Prints the decompostion tree into file.]

Description []

SideEffects []

SeeAlso []

Definition at line 830 of file dsdTree.c.

{
    Dsd_Node_t * pNode;
    int SigCounter;
    int i;
    SigCounter = 1;
 
    if ( Output == -1 )
    {
        for ( i = 0; i < pDsdMan->nRoots; i++ )
        {
            pNode = Dsd_Regular( pDsdMan->pRoots[i] );
            Dsd_TreePrint_rec( pFile, pNode, (pNode != pDsdMan->pRoots[i]), pInputNames, pOutputNames[i], OffSet, &SigCounter, fShortNames );
        }
    }
    else
    {
        assert( Output >= 0 && Output < pDsdMan->nRoots );
        pNode = Dsd_Regular( pDsdMan->pRoots[Output] );
        Dsd_TreePrint_rec( pFile, pNode, (pNode != pDsdMan->pRoots[Output]), pInputNames, pOutputNames[Output], OffSet, &SigCounter, fShortNames );
    }
}

Here is the caller graph for this function:

Dsd_TreePrint2()

void Dsd_TreePrint2	(	FILE *	pFile,
		Dsd_Manager_t *	pDsdMan,
		char *	pInputNames[],
		char *	pOutputNames[],
		int	Output )

Definition at line 1106 of file dsdTree.c.

{
    if ( Output == -1 )
    {
        int i;
        for ( i = 0; i < pDsdMan->nRoots; i++ )
        {
            fprintf( pFile, "%8s = ", pOutputNames[i] );
            Dsd_TreePrint2_rec( pFile, pDsdMan->dd, Dsd_Regular(pDsdMan->pRoots[i]), Dsd_IsComplement(pDsdMan->pRoots[i]), pInputNames );
            fprintf( pFile, "\n" );
        }
    }
    else
    {
        assert( Output >= 0 && Output < pDsdMan->nRoots );
        fprintf( pFile, "%8s = ", pOutputNames[Output] );
        Dsd_TreePrint2_rec( pFile, pDsdMan->dd, Dsd_Regular(pDsdMan->pRoots[Output]), Dsd_IsComplement(pDsdMan->pRoots[Output]), pInputNames );
        fprintf( pFile, "\n" );
    }
}

Here is the call graph for this function:

Dsd_TreePrint2_rec()

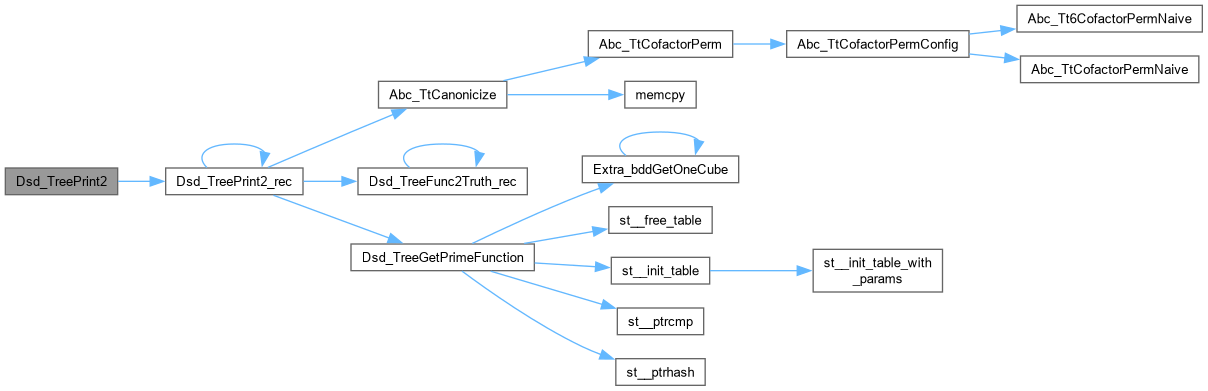
void Dsd_TreePrint2_rec	(	FILE *	pFile,
		DdManager *	dd,
		Dsd_Node_t *	pNode,
		int	fComp,
		char *	pInputNames[] )

Definition at line 1042 of file dsdTree.c.

{
    int i;
    if ( pNode->Type == DSD_NODE_CONST1 )
    {
        fprintf( pFile, "Const%d", !fComp );
        return;
    }
    assert( pNode->Type == DSD_NODE_BUF || pNode->Type == DSD_NODE_PRIME || pNode->Type == DSD_NODE_OR || pNode->Type == DSD_NODE_EXOR ); 
//    fprintf( pFile, "%s", (fComp ^ (pNode->Type == DSD_NODE_OR))? "!" : "" );
    if ( pNode->Type == DSD_NODE_BUF )
    {
        fprintf( pFile, "%s", fComp? "!" : "" );
        fprintf( pFile, "%s", pInputNames[pNode->S->index] );
    }
    else if ( pNode->Type == DSD_NODE_PRIME )
    {
        fprintf( pFile, " " );
        if ( pNode->nDecs <= 6 )
        {
            char pCanonPerm[6]; int uCanonPhase;
            // compute truth table
            DdNode * bFunc = Dsd_TreeGetPrimeFunction( dd, pNode );  
            word uTruth = Dsd_TreeFunc2Truth_rec( dd, bFunc );
            Cudd_Ref( bFunc );
            Cudd_RecursiveDeref( dd, bFunc );
            // canonicize truth table
            uCanonPhase = Abc_TtCanonicize( &uTruth, pNode->nDecs, pCanonPerm );
            fprintf( pFile, "%s", (fComp ^ ((uCanonPhase >> pNode->nDecs) & 1)) ? "!" : "" );
            Abc_TtPrintHexRev( pFile, &uTruth, pNode->nDecs );
            fprintf( pFile, "{" );
            for ( i = 0; i < pNode->nDecs; i++ )
            {
                Dsd_Node_t * pInput = pNode->pDecs[(int)pCanonPerm[i]];
                Dsd_TreePrint2_rec( pFile, dd, Dsd_Regular(pInput), Dsd_IsComplement(pInput) ^ ((uCanonPhase>>i)&1), pInputNames );
            }
            fprintf( pFile, "} " );
        }
        else
        {
            fprintf( pFile, "|%d|", pNode->nDecs );
            fprintf( pFile, "{" );
            for ( i = 0; i < pNode->nDecs; i++ )
                Dsd_TreePrint2_rec( pFile, dd, Dsd_Regular(pNode->pDecs[i]), Dsd_IsComplement(pNode->pDecs[i]), pInputNames );
            fprintf( pFile, "} " );
        }
    }
    else if ( pNode->Type == DSD_NODE_OR )
    {
        fprintf( pFile, "%s", !fComp? "!" : "" );
        fprintf( pFile, "(" );
        for ( i = 0; i < pNode->nDecs; i++ )
            Dsd_TreePrint2_rec( pFile, dd, Dsd_Regular(pNode->pDecs[i]), !Dsd_IsComplement(pNode->pDecs[i]), pInputNames );
        fprintf( pFile, ")" );
    }
    else if ( pNode->Type == DSD_NODE_EXOR )
    {
        fprintf( pFile, "%s", fComp? "!" : "" );
        fprintf( pFile, "[" );
        for ( i = 0; i < pNode->nDecs; i++ )
            Dsd_TreePrint2_rec( pFile, dd, Dsd_Regular(pNode->pDecs[i]), Dsd_IsComplement(pNode->pDecs[i]), pInputNames );
        fprintf( pFile, "]" );
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreePrint3()

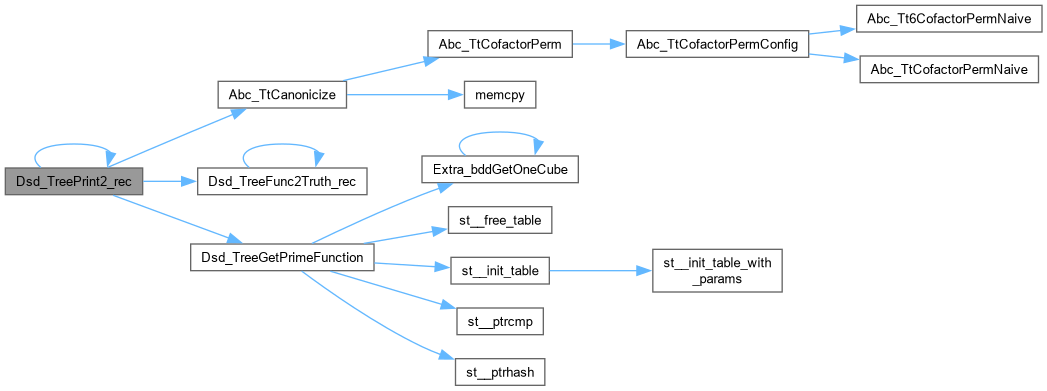
void Dsd_TreePrint3	(	void *	pStr,
		Dsd_Manager_t *	pDsdMan,
		int	Output )

Definition at line 748 of file dsdTree.c.

{
    Vec_Str_t * p = (Vec_Str_t *)pStr;
    assert( Output >= 0 && Output < pDsdMan->nRoots );
    Dsd_Node_t * pNode = Dsd_Regular( pDsdMan->pRoots[Output] );
    int fCompl = pNode != pDsdMan->pRoots[Output];
    if ( pNode->Type == DSD_NODE_CONST1 ) 
        Vec_StrPush( p, fCompl ? '0' : '1' );
    else {
        if ( fCompl )
            Vec_StrPush( p, '~' );
        Dsd_TreePrint3_rec( p, pNode );
    }    
    Vec_StrPush( p, '\0' );
}

Here is the call graph for this function:

Dsd_TreePrint3_rec()

void Dsd_TreePrint3_rec	(	Vec_Str_t *	p,
		Dsd_Node_t *	pNode )

Function*************************************************************

Synopsis [Prints the decompostion tree into a string.]

Description []

SideEffects []

SeeAlso []

Definition at line 720 of file dsdTree.c.

{
    if ( pNode->Type == DSD_NODE_BUF ) {
        Vec_StrPush( p, (int)(pNode->S->index >= 26 ? 'A' - 26 : 'a') + pNode->S->index );
        return;
    }
    if ( pNode->Type == DSD_NODE_PRIME )
        Vec_StrPush( p, '{' );
    else if ( pNode->Type == DSD_NODE_OR )
        Vec_StrPush( p, '(' );
    else if ( pNode->Type == DSD_NODE_EXOR )
        Vec_StrPush( p, '[' );
    else assert( 0 );
    for ( int i = 0; i < pNode->nDecs; i++ )
    {
        Dsd_Node_t * pInput = Dsd_Regular( pNode->pDecs[i] );
        if ( pInput != pNode->pDecs[i] )
            Vec_StrPush( p, '~' );
        Dsd_TreePrint3_rec( p, pInput );
    }
    if ( pNode->Type == DSD_NODE_PRIME )
        Vec_StrPush( p, '}' );
    else if ( pNode->Type == DSD_NODE_OR )
        Vec_StrPush( p, ')' );
    else if ( pNode->Type == DSD_NODE_EXOR )
        Vec_StrPush( p, ']' );
    else assert( 0 );
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreePrint4()

void Dsd_TreePrint4	(	void *	pStr,
		Dsd_Manager_t *	pDsdMan,
		int	Output )

Definition at line 803 of file dsdTree.c.

{
    Vec_Str_t * p = (Vec_Str_t *)pStr;
    assert( Output >= 0 && Output < pDsdMan->nRoots );
    Dsd_Node_t * pNode = Dsd_Regular( pDsdMan->pRoots[Output] );
    int fCompl = pNode != pDsdMan->pRoots[Output];
    if ( pNode->Type == DSD_NODE_CONST1 ) 
        Vec_StrPush( p, fCompl ? '0' : '1' );
    else {
        if ( fCompl ^ (pNode->Type == DSD_NODE_OR) )
            Vec_StrPush( p, '~' );
        Dsd_TreePrint4_rec( p, pNode );
    }    
    Vec_StrPush( p, '\0' );
}

Here is the call graph for this function:

Dsd_TreePrint4_rec()

void Dsd_TreePrint4_rec	(	Vec_Str_t *	p,
		Dsd_Node_t *	pNode )

Function*************************************************************

Synopsis [Prints the decompostion tree into a string.]

Description []

SideEffects []

SeeAlso []

Definition at line 775 of file dsdTree.c.

{
    if ( pNode->Type == DSD_NODE_BUF ) {
        Vec_StrPush( p, (int)(pNode->S->index >= 26 ? 'A' - 26 : 'a') + pNode->S->index );
        return;
    }
    if ( pNode->Type == DSD_NODE_PRIME )
        Vec_StrPush( p, '{' );
    else if ( pNode->Type == DSD_NODE_OR )
        Vec_StrPush( p, '(' );
    else if ( pNode->Type == DSD_NODE_EXOR )
        Vec_StrPush( p, '[' );
    else assert( 0 );
    for ( int i = 0; i < pNode->nDecs; i++ )
    {
        Dsd_Node_t * pInput = Dsd_Regular( pNode->pDecs[i] );
        if ( (pInput != pNode->pDecs[i]) ^ (pNode->Type == DSD_NODE_OR) ^ (pInput->Type == DSD_NODE_OR) )
            Vec_StrPush( p, '~' );
        Dsd_TreePrint4_rec( p, pInput );
    }
    if ( pNode->Type == DSD_NODE_PRIME )
        Vec_StrPush( p, '}' );
    else if ( pNode->Type == DSD_NODE_OR )
        Vec_StrPush( p, ')' );
    else if ( pNode->Type == DSD_NODE_EXOR )
        Vec_StrPush( p, ']' );
    else assert( 0 );
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreeSuppSize()

int Dsd_TreeSuppSize	(	Dsd_Manager_t *	pDsdMan,
		int	Output )

Definition at line 693 of file dsdTree.c.

{
    if ( Output == -1 ) 
    {
        int i, Res = 0;
        for ( i = 0; i < pDsdMan->nRoots; i++ )
            Res += Dsd_TreeSuppSize_rec( Dsd_Regular( pDsdMan->pRoots[i] ) );
        return Res;
    }
    else 
    {
        assert( Output >= 0 && Output < pDsdMan->nRoots );
        return Dsd_TreeSuppSize_rec( Dsd_Regular( pDsdMan->pRoots[Output] ) );
    }
}

Here is the call graph for this function:

Dsd_TreeSuppSize_rec()

int Dsd_TreeSuppSize_rec

(

Dsd_Node_t *

pNode

)

Function*************************************************************

Synopsis [Returns the support size.]

Description []

SideEffects []

SeeAlso []

Definition at line 682 of file dsdTree.c.

{
    if ( pNode->Type == DSD_NODE_CONST1 )
        return 0;
    if ( pNode->Type == DSD_NODE_BUF )
        return 1;
    int nSuppSize = 0;
    for ( int i = 0; i < pNode->nDecs; i++ )
        nSuppSize += Dsd_TreeSuppSize_rec( Dsd_Regular( pNode->pDecs[i] ) );
    return nSuppSize;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Dsd_TreeUnmark()

void Dsd_TreeUnmark

(

Dsd_Manager_t *

pDsdMan

)

Function*************************************************************

Synopsis [Unmarks the decomposition tree.]

Description [This function assumes that originally pNode->nVisits are set to zero!]

SideEffects []

SeeAlso []

Definition at line 107 of file dsdTree.c.

{
    int i;
    for ( i = 0; i < pDsdMan->nRoots; i++ )
        Dsd_TreeUnmark_rec( Dsd_Regular( pDsdMan->pRoots[i] ) );
}

Here is the caller graph for this function: