ABC: A System for Sequential Synthesis and Verification
 
Loading...
Searching...
No Matches
Macros | Typedefs | Functions
utilIsop.c File Reference
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
#include "misc/vec/vec.h"
#include "misc/util/utilTruth.h"
Include dependency graph for utilIsop.c:

Go to the source code of this file.

Macros

#define ABC_ISOP_MAX_VAR   16
 DECLARATIONS ///.
 
#define ABC_ISOP_MAX_WORD   (ABC_ISOP_MAX_VAR > 6 ? (1 << (ABC_ISOP_MAX_VAR-6)) : 1)
 
#define ABC_ISOP_MAX_CUBE   0xFFFF
 

Typedefs

typedef word FUNC_ISOP(word *, word *, word *, word, int *)
 

Functions

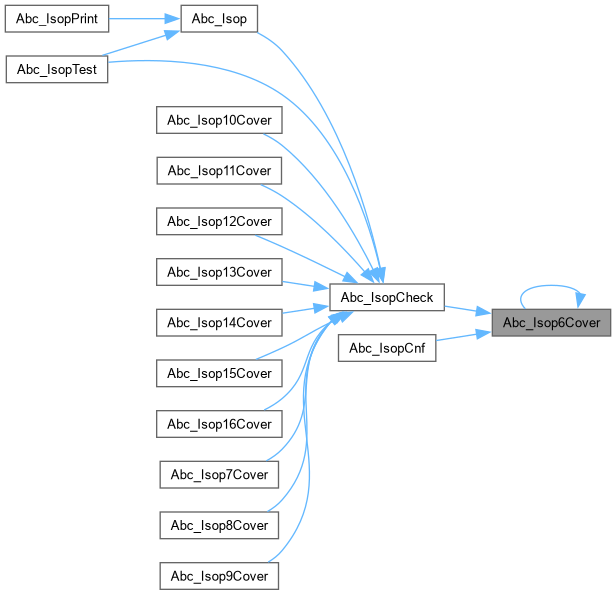
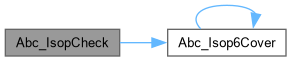
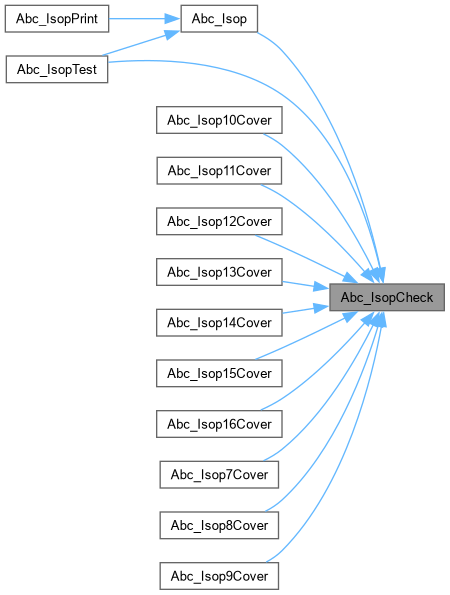
word Abc_IsopCheck (word *pOn, word *pOnDc, word *pRes, int nVars, word CostLim, int *pCover)
 
word Abc_EsopCheck (word *pOn, int nVars, word CostLim, int *pCover)
 
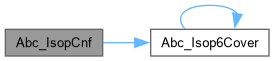
word Abc_Isop6Cover (word uOn, word uOnDc, word *pRes, int nVars, word CostLim, int *pCover)
 
word Abc_Isop7Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop8Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop9Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop10Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop11Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop12Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop13Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop14Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop15Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
word Abc_Isop16Cover (word *pOn, word *pOnDc, word *pRes, word CostLim, int *pCover)
 
void Abc_IsopBuildTruth (Vec_Int_t *vCover, int nVars, word *pRes, int fXor, int fCompl)
 
int Abc_Isop (word *pFunc, int nVars, int nCubeLim, Vec_Int_t *vCover, int fTryBoth)
 
int Abc_IsopCnf (word *pFunc, int nVars, int nCubeLim, int *pCover)
 
int Abc_IsopCountLits (Vec_Int_t *vCover, int nVars)
 
void Abc_IsopPrintCover (Vec_Int_t *vCover, int nVars, int fCompl)
 
void Abc_IsopPrint (word *t, int nVars, Vec_Int_t *vCover, int fTryBoth)
 
word Abc_Esop6Cover (word t, int nVars, word CostLim, int *pCover)
 
word Abc_EsopCover (word *pOn, int nVars, word CostLim, int *pCover)
 
word Abc_IsopNew (word *pOn, word *pOnDc, word *pRes, int nVars, word CostLim, int *pCover)
 
void Abc_IsopTestNew ()
 
int Abc_IsopTest (word *pFunc, int nVars, Vec_Int_t *vCover)
 

Macro Definition Documentation

◆ ABC_ISOP_MAX_CUBE

#define ABC_ISOP_MAX_CUBE   0xFFFF

Definition at line 37 of file utilIsop.c.

◆ ABC_ISOP_MAX_VAR

#define ABC_ISOP_MAX_VAR   16

DECLARATIONS ///.

CFile****************************************************************

FileName [utilIsop.c]

SystemName [ABC: Logic synthesis and verification system.]

PackageName [ISOP computation.]

Synopsis [ISOP computation.]

Author [Alan Mishchenko]

Affiliation [UC Berkeley]

Date [Ver. 1.0. Started - October 4, 2014.]

Revision [

Id
utilIsop.c,v 1.00 2014/10/04 00:00:00 alanmi Exp

]

Definition at line 35 of file utilIsop.c.

◆ ABC_ISOP_MAX_WORD

#define ABC_ISOP_MAX_WORD   (ABC_ISOP_MAX_VAR > 6 ? (1 << (ABC_ISOP_MAX_VAR-6)) : 1)

Definition at line 36 of file utilIsop.c.

Typedef Documentation

◆ FUNC_ISOP

typedef word FUNC_ISOP(word *, word *, word *, word, int *)

Definition at line 39 of file utilIsop.c.

Function Documentation

◆ Abc_Esop6Cover()

word Abc_Esop6Cover ( word t,
int nVars,
word CostLim,
int * pCover )

Definition at line 713 of file utilIsop.c.

714{
715 word c0, c1;
716 word r0, r1, r2, Max;
717 int Var;
718 assert( nVars <= 6 );
719 if ( t == 0 )
720 return 0;
721 if ( t == ~(word)0 )
722 {
723 if ( pCover ) *pCover = 0;
724 return Abc_Cube2Cost(1);
725 }
726 assert( nVars > 0 );
727 // find the topmost var
728 for ( Var = nVars-1; Var >= 0; Var-- )
729 if ( Abc_Tt6HasVar( t, Var ) )
730 break;
731 assert( Var >= 0 );
732 // cofactor
733 c0 = Abc_Tt6Cofactor0( t, Var );
734 c1 = Abc_Tt6Cofactor1( t, Var );
735 // call recursively
736 r0 = Abc_Esop6Cover( c0, Var, CostLim, pCover ? pCover : NULL );
737 if ( r0 >= CostLim ) return CostLim;
738 r1 = Abc_Esop6Cover( c1, Var, CostLim, pCover ? pCover + Abc_CostCubes(r0) : NULL );
739 if ( r1 >= CostLim ) return CostLim;
740 r2 = Abc_Esop6Cover( c0 ^ c1, Var, CostLim, pCover ? pCover + Abc_CostCubes(r0) + Abc_CostCubes(r1) : NULL );
741 if ( r2 >= CostLim ) return CostLim;
742 Max = Abc_MaxWord( r0, Abc_MaxWord(r1, r2) );
743 if ( r0 + r1 + r2 - Max >= CostLim ) return CostLim;
744 return r0 + r1 + r2 - Max + Abc_EsopAddLits( pCover, r0, r1, r2, Max, Var );
745}
Var
int Var
Definition exorList.c:228
word
unsigned __int64 word
DECLARATIONS ///.
Definition kitPerm.c:36
Abc_Esop6Cover
word Abc_Esop6Cover(word t, int nVars, word CostLim, int *pCover)
Definition utilIsop.c:713
assert
#define assert(ex)
Definition util_old.h:213
Here is the call graph for this function:
Here is the caller graph for this function:

◆ Abc_EsopCheck()

word Abc_EsopCheck ( word * pOn,
int nVars,
word CostLim,
int * pCover )
extern

Definition at line 766 of file utilIsop.c.

767{
768 int nVarsNew; word Cost;
769 if ( nVars <= 6 )
770 return Abc_Esop6Cover( *pOn, nVars, CostLim, pCover );
771 for ( nVarsNew = nVars; nVarsNew > 6; nVarsNew-- )
772 if ( Abc_TtHasVar( pOn, nVars, nVarsNew-1 ) )
773 break;
774 if ( nVarsNew == 6 )
775 Cost = Abc_Esop6Cover( *pOn, nVarsNew, CostLim, pCover );
776 else
777 Cost = Abc_EsopCover( pOn, nVarsNew, CostLim, pCover );
778 return Cost;
779}
Abc_EsopCover
word Abc_EsopCover(word *pOn, int nVars, word CostLim, int *pCover)
Definition utilIsop.c:746
Here is the call graph for this function:
Here is the caller graph for this function:

◆ Abc_EsopCover()

word Abc_EsopCover ( word * pOn,
int nVars,
word CostLim,
int * pCover )

Definition at line 746 of file utilIsop.c.

747{
748 word r0, r1, r2, Max;
749 int c, nWords = (1 << (nVars - 7));
750 assert( nVars > 6 );
751 assert( Abc_TtHasVar( pOn, nVars, nVars - 1 ) );
752 r0 = Abc_EsopCheck( pOn, nVars-1, CostLim, pCover );
753 if ( r0 >= CostLim ) return CostLim;
754 r1 = Abc_EsopCheck( pOn+nWords, nVars-1, CostLim, pCover ? pCover + Abc_CostCubes(r0) : NULL );
755 if ( r1 >= CostLim ) return CostLim;
756 for ( c = 0; c < nWords; c++ )
757 pOn[c] ^= pOn[nWords+c];
758 r2 = Abc_EsopCheck( pOn, nVars-1, CostLim, pCover ? pCover + Abc_CostCubes(r0) + Abc_CostCubes(r1) : NULL );
759 for ( c = 0; c < nWords; c++ )
760 pOn[c] ^= pOn[nWords+c];
761 if ( r2 >= CostLim ) return CostLim;
762 Max = Abc_MaxWord( r0, Abc_MaxWord(r1, r2) );
763 if ( r0 + r1 + r2 - Max >= CostLim ) return CostLim;
764 return r0 + r1 + r2 - Max + Abc_EsopAddLits( pCover, r0, r1, r2, Max, nVars-1 );
765}
nWords
int nWords
Definition abcNpn.c:127
Abc_EsopCheck
word Abc_EsopCheck(word *pOn, int nVars, word CostLim, int *pCover)
Definition utilIsop.c:766
Here is the call graph for this function:
Here is the caller graph for this function:

◆ Abc_Isop()

int Abc_Isop ( word * pFunc,
int nVars,
int nCubeLim,
Vec_Int_t * vCover,
int fTryBoth )

Function*************************************************************

Synopsis [This procedure assumes that function has exact support.]

Description []

SideEffects []

SeeAlso []

Definition at line 511 of file utilIsop.c.

512{
513 word pRes[ABC_ISOP_MAX_WORD];
514 word Cost0, Cost1, Cost, CostInit = Abc_Cube2Cost(nCubeLim);
515 assert( nVars <= ABC_ISOP_MAX_VAR );
516 Vec_IntGrow( vCover, 1 << (nVars-1) );
517 if ( fTryBoth )
518 {
519 Cost0 = Abc_IsopCheck( pFunc, pFunc, pRes, nVars, CostInit, NULL );
520 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
521 Cost1 = Abc_IsopCheck( pFunc, pFunc, pRes, nVars, Cost0, NULL );
522 Cost = Abc_MinWord( Cost0, Cost1 );
523 if ( Cost == CostInit )
524 {
525 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
526 return -1;
527 }
528 if ( Cost == Cost0 )
529 {
530 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
531 Abc_IsopCheck( pFunc, pFunc, pRes, nVars, CostInit, Vec_IntArray(vCover) );
532 }
533 else // if ( Cost == Cost1 )
534 {
535 Abc_IsopCheck( pFunc, pFunc, pRes, nVars, CostInit, Vec_IntArray(vCover) );
536 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
537 }
538 }
539 else
540 {
541 Cost = Cost0 = Abc_IsopCheck( pFunc, pFunc, pRes, nVars, CostInit, Vec_IntArray(vCover) );
542 if ( Cost == CostInit )
543 return -1;
544 }
545 vCover->nSize = Abc_CostCubes(Cost);
546 assert( vCover->nSize <= vCover->nCap );
547// Abc_IsopVerify( pFunc, nVars, pRes, vCover, 0, Cost != Cost0 );
548 return Cost != Cost0;
549}
ABC_ISOP_MAX_VAR
#define ABC_ISOP_MAX_VAR
DECLARATIONS ///.
Definition utilIsop.c:35
Abc_IsopCheck
word Abc_IsopCheck(word *pOn, word *pOnDc, word *pRes, int nVars, word CostLim, int *pCover)
Definition utilIsop.c:428
ABC_ISOP_MAX_WORD
#define ABC_ISOP_MAX_WORD
Definition utilIsop.c:36
Here is the call graph for this function:
Here is the caller graph for this function:

◆ Abc_Isop10Cover()

word Abc_Isop10Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 232 of file utilIsop.c.

233{
234 word uOn2[8], uOnDc2[8], uRes0[8], uRes1[8], uRes2[8];
235 word Cost0, Cost1, Cost2; int c, nVars = 9, nWords = 8;
236 // negative cofactor
237 for ( c = 0; c < nWords; c++ )
238 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
239 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
240 if ( Cost0 >= CostLim ) return CostLim;
241 // positive cofactor
242 for ( c = 0; c < nWords; c++ )
243 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
244 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
245 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
246 // middle cofactor
247 for ( c = 0; c < nWords; c++ )
248 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
249 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
250 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
251 // derive the final truth table
252 for ( c = 0; c < nWords; c++ )
253 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
254 // verify
255 for ( c = 0; c < (nWords<<1); c++ )
256 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
257 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
258 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
259}
Here is the call graph for this function:

◆ Abc_Isop11Cover()

word Abc_Isop11Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 260 of file utilIsop.c.

261{
262 word uOn2[16], uOnDc2[16], uRes0[16], uRes1[16], uRes2[16];
263 word Cost0, Cost1, Cost2; int c, nVars = 10, nWords = 16;
264 // negative cofactor
265 for ( c = 0; c < nWords; c++ )
266 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
267 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
268 if ( Cost0 >= CostLim ) return CostLim;
269 // positive cofactor
270 for ( c = 0; c < nWords; c++ )
271 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
272 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
273 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
274 // middle cofactor
275 for ( c = 0; c < nWords; c++ )
276 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
277 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
278 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
279 // derive the final truth table
280 for ( c = 0; c < nWords; c++ )
281 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
282 // verify
283 for ( c = 0; c < (nWords<<1); c++ )
284 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
285 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
286 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
287}
Here is the call graph for this function:

◆ Abc_Isop12Cover()

word Abc_Isop12Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 288 of file utilIsop.c.

289{
290 word uOn2[32], uOnDc2[32], uRes0[32], uRes1[32], uRes2[32];
291 word Cost0, Cost1, Cost2; int c, nVars = 11, nWords = 32;
292 // negative cofactor
293 for ( c = 0; c < nWords; c++ )
294 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
295 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
296 if ( Cost0 >= CostLim ) return CostLim;
297 // positive cofactor
298 for ( c = 0; c < nWords; c++ )
299 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
300 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
301 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
302 // middle cofactor
303 for ( c = 0; c < nWords; c++ )
304 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
305 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
306 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
307 // derive the final truth table
308 for ( c = 0; c < nWords; c++ )
309 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
310 // verify
311 for ( c = 0; c < (nWords<<1); c++ )
312 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
313 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
314 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
315}
Here is the call graph for this function:

◆ Abc_Isop13Cover()

word Abc_Isop13Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 316 of file utilIsop.c.

317{
318 word uOn2[64], uOnDc2[64], uRes0[64], uRes1[64], uRes2[64];
319 word Cost0, Cost1, Cost2; int c, nVars = 12, nWords = 64;
320 // negative cofactor
321 for ( c = 0; c < nWords; c++ )
322 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
323 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
324 if ( Cost0 >= CostLim ) return CostLim;
325 // positive cofactor
326 for ( c = 0; c < nWords; c++ )
327 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
328 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
329 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
330 // middle cofactor
331 for ( c = 0; c < nWords; c++ )
332 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
333 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
334 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
335 // derive the final truth table
336 for ( c = 0; c < nWords; c++ )
337 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
338 // verify
339 for ( c = 0; c < (nWords<<1); c++ )
340 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
341 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
342 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
343}
Here is the call graph for this function:

◆ Abc_Isop14Cover()

word Abc_Isop14Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 344 of file utilIsop.c.

345{
346 word uOn2[128], uOnDc2[128], uRes0[128], uRes1[128], uRes2[128];
347 word Cost0, Cost1, Cost2; int c, nVars = 13, nWords = 128;
348 // negative cofactor
349 for ( c = 0; c < nWords; c++ )
350 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
351 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
352 if ( Cost0 >= CostLim ) return CostLim;
353 // positive cofactor
354 for ( c = 0; c < nWords; c++ )
355 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
356 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
357 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
358 // middle cofactor
359 for ( c = 0; c < nWords; c++ )
360 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
361 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
362 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
363 // derive the final truth table
364 for ( c = 0; c < nWords; c++ )
365 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
366 // verify
367 for ( c = 0; c < (nWords<<1); c++ )
368 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
369 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
370 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
371}
Here is the call graph for this function:

◆ Abc_Isop15Cover()

word Abc_Isop15Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 372 of file utilIsop.c.

373{
374 word uOn2[256], uOnDc2[256], uRes0[256], uRes1[256], uRes2[256];
375 word Cost0, Cost1, Cost2; int c, nVars = 14, nWords = 256;
376 // negative cofactor
377 for ( c = 0; c < nWords; c++ )
378 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
379 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
380 if ( Cost0 >= CostLim ) return CostLim;
381 // positive cofactor
382 for ( c = 0; c < nWords; c++ )
383 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
384 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
385 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
386 // middle cofactor
387 for ( c = 0; c < nWords; c++ )
388 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
389 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
390 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
391 // derive the final truth table
392 for ( c = 0; c < nWords; c++ )
393 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
394 // verify
395 for ( c = 0; c < (nWords<<1); c++ )
396 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
397 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
398 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
399}
Here is the call graph for this function:

◆ Abc_Isop16Cover()

word Abc_Isop16Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 400 of file utilIsop.c.

401{
402 word uOn2[512], uOnDc2[512], uRes0[512], uRes1[512], uRes2[512];
403 word Cost0, Cost1, Cost2; int c, nVars = 15, nWords = 512;
404 // negative cofactor
405 for ( c = 0; c < nWords; c++ )
406 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
407 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
408 if ( Cost0 >= CostLim ) return CostLim;
409 // positive cofactor
410 for ( c = 0; c < nWords; c++ )
411 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
412 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
413 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
414 // middle cofactor
415 for ( c = 0; c < nWords; c++ )
416 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
417 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
418 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
419 // derive the final truth table
420 for ( c = 0; c < nWords; c++ )
421 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
422 // verify
423 for ( c = 0; c < (nWords<<1); c++ )
424 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
425 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
426 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
427}
Here is the call graph for this function:

◆ Abc_Isop6Cover()

word Abc_Isop6Cover ( word uOn,
word uOnDc,
word * pRes,
int nVars,
word CostLim,
int * pCover )

Definition at line 108 of file utilIsop.c.

109{
110 word uOn0, uOn1, uOnDc0, uOnDc1, uRes0, uRes1, uRes2;
111 word Cost0, Cost1, Cost2; int Var;
112 assert( nVars <= 6 );
113 assert( (uOn & ~uOnDc) == 0 );
114 if ( uOn == 0 )
115 {
116 pRes[0] = 0;
117 return 0;
118 }
119 if ( uOnDc == ~(word)0 )
120 {
121 pRes[0] = ~(word)0;
122 if ( pCover ) pCover[0] = 0;
123 return Abc_Cube2Cost(1);
124 }
125 assert( nVars > 0 );
126 // find the topmost var
127 for ( Var = nVars-1; Var >= 0; Var-- )
128 if ( Abc_Tt6HasVar( uOn, Var ) || Abc_Tt6HasVar( uOnDc, Var ) )
129 break;
130 assert( Var >= 0 );
131 // cofactor
132 uOn0 = Abc_Tt6Cofactor0( uOn, Var );
133 uOn1 = Abc_Tt6Cofactor1( uOn , Var );
134 uOnDc0 = Abc_Tt6Cofactor0( uOnDc, Var );
135 uOnDc1 = Abc_Tt6Cofactor1( uOnDc, Var );
136 // solve for cofactors
137 Cost0 = Abc_Isop6Cover( uOn0 & ~uOnDc1, uOnDc0, &uRes0, Var, CostLim, pCover );
138 if ( Cost0 >= CostLim ) return CostLim;
139 Cost1 = Abc_Isop6Cover( uOn1 & ~uOnDc0, uOnDc1, &uRes1, Var, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
140 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
141 Cost2 = Abc_Isop6Cover( (uOn0 & ~uRes0) | (uOn1 & ~uRes1), uOnDc0 & uOnDc1, &uRes2, Var, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
142 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
143 // derive the final truth table
144 *pRes = uRes2 | (uRes0 & s_Truths6Neg[Var]) | (uRes1 & s_Truths6[Var]);
145 assert( (uOn & ~*pRes) == 0 && (*pRes & ~uOnDc) == 0 );
146 Abc_IsopAddLits( pCover, Cost0, Cost1, Var );
147 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
148}
Abc_Isop6Cover
word Abc_Isop6Cover(word uOn, word uOnDc, word *pRes, int nVars, word CostLim, int *pCover)
Definition utilIsop.c:108
Here is the call graph for this function:
Here is the caller graph for this function:

◆ Abc_Isop7Cover()

word Abc_Isop7Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 149 of file utilIsop.c.

150{
151 word uOn0, uOn1, uOn2, uOnDc2, uRes0, uRes1, uRes2;
152 word Cost0, Cost1, Cost2; int nVars = 6;
153 assert( (pOn[0] & ~pOnDc[0]) == 0 );
154 assert( (pOn[1] & ~pOnDc[1]) == 0 );
155 // cofactor
156 uOn0 = pOn[0] & ~pOnDc[1];
157 uOn1 = pOn[1] & ~pOnDc[0];
158 // solve for cofactors
159 Cost0 = Abc_IsopCheck( &uOn0, pOnDc, &uRes0, nVars, CostLim, pCover );
160 if ( Cost0 >= CostLim ) return CostLim;
161 Cost1 = Abc_IsopCheck( &uOn1, pOnDc+1, &uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
162 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
163 uOn2 = (pOn[0] & ~uRes0) | (pOn[1] & ~uRes1);
164 uOnDc2 = pOnDc[0] & pOnDc[1];
165 Cost2 = Abc_IsopCheck( &uOn2, &uOnDc2, &uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
166 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
167 // derive the final truth table
168 pRes[0] = uRes2 | uRes0;
169 pRes[1] = uRes2 | uRes1;
170 assert( (pOn[0] & ~pRes[0]) == 0 && (pRes[0] & ~pOnDc[0]) == 0 );
171 assert( (pOn[1] & ~pRes[1]) == 0 && (pRes[1] & ~pOnDc[1]) == 0 );
172 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
173 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
174}
Here is the call graph for this function:

◆ Abc_Isop8Cover()

word Abc_Isop8Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 175 of file utilIsop.c.

176{
177 word uOn2[2], uOnDc2[2], uRes0[2], uRes1[2], uRes2[2];
178 word Cost0, Cost1, Cost2; int nVars = 7;
179 // negative cofactor
180 uOn2[0] = pOn[0] & ~pOnDc[2];
181 uOn2[1] = pOn[1] & ~pOnDc[3];
182 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
183 if ( Cost0 >= CostLim ) return CostLim;
184 // positive cofactor
185 uOn2[0] = pOn[2] & ~pOnDc[0];
186 uOn2[1] = pOn[3] & ~pOnDc[1];
187 Cost1 = Abc_IsopCheck( uOn2, pOnDc+2, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
188 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
189 // middle cofactor
190 uOn2[0] = (pOn[0] & ~uRes0[0]) | (pOn[2] & ~uRes1[0]); uOnDc2[0] = pOnDc[0] & pOnDc[2];
191 uOn2[1] = (pOn[1] & ~uRes0[1]) | (pOn[3] & ~uRes1[1]); uOnDc2[1] = pOnDc[1] & pOnDc[3];
192 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
193 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
194 // derive the final truth table
195 pRes[0] = uRes2[0] | uRes0[0];
196 pRes[1] = uRes2[1] | uRes0[1];
197 pRes[2] = uRes2[0] | uRes1[0];
198 pRes[3] = uRes2[1] | uRes1[1];
199 assert( (pOn[0] & ~pRes[0]) == 0 && (pOn[1] & ~pRes[1]) == 0 && (pOn[2] & ~pRes[2]) == 0 && (pOn[3] & ~pRes[3]) == 0 );
200 assert( (pRes[0] & ~pOnDc[0])==0 && (pRes[1] & ~pOnDc[1])==0 && (pRes[2] & ~pOnDc[2])==0 && (pRes[3] & ~pOnDc[3])==0 );
201 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
202 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
203}
Here is the call graph for this function:

◆ Abc_Isop9Cover()

word Abc_Isop9Cover ( word * pOn,
word * pOnDc,
word * pRes,
word CostLim,
int * pCover )

Definition at line 204 of file utilIsop.c.

205{
206 word uOn2[4], uOnDc2[4], uRes0[4], uRes1[4], uRes2[4];
207 word Cost0, Cost1, Cost2; int c, nVars = 8, nWords = 4;
208 // negative cofactor
209 for ( c = 0; c < nWords; c++ )
210 uOn2[c] = pOn[c] & ~pOnDc[c+nWords];
211 Cost0 = Abc_IsopCheck( uOn2, pOnDc, uRes0, nVars, CostLim, pCover );
212 if ( Cost0 >= CostLim ) return CostLim;
213 // positive cofactor
214 for ( c = 0; c < nWords; c++ )
215 uOn2[c] = pOn[c+nWords] & ~pOnDc[c];
216 Cost1 = Abc_IsopCheck( uOn2, pOnDc+nWords, uRes1, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
217 if ( Cost0 + Cost1 >= CostLim ) return CostLim;
218 // middle cofactor
219 for ( c = 0; c < nWords; c++ )
220 uOn2[c] = (pOn[c] & ~uRes0[c]) | (pOn[c+nWords] & ~uRes1[c]), uOnDc2[c] = pOnDc[c] & pOnDc[c+nWords];
221 Cost2 = Abc_IsopCheck( uOn2, uOnDc2, uRes2, nVars, CostLim, pCover ? pCover + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1) : NULL );
222 if ( Cost0 + Cost1 + Cost2 >= CostLim ) return CostLim;
223 // derive the final truth table
224 for ( c = 0; c < nWords; c++ )
225 pRes[c] = uRes2[c] | uRes0[c], pRes[c+nWords] = uRes2[c] | uRes1[c];
226 // verify
227 for ( c = 0; c < (nWords<<1); c++ )
228 assert( (pOn[c] & ~pRes[c] ) == 0 && (pRes[c] & ~pOnDc[c]) == 0 );
229 Abc_IsopAddLits( pCover, Cost0, Cost1, nVars );
230 return Cost0 + Cost1 + Cost2 + Abc_CostCubes(Cost0) + Abc_CostCubes(Cost1);
231}
Here is the call graph for this function:

◆ Abc_IsopBuildTruth()

void Abc_IsopBuildTruth ( Vec_Int_t * vCover,
int nVars,
word * pRes,
int fXor,
int fCompl )

Definition at line 467 of file utilIsop.c.

468{
469 word ** pTtElems = Abc_IsopTtElems();
470 word pCube[ABC_ISOP_MAX_WORD];
471 int nWords = Abc_TtWordNum( nVars );
472 int c, v, Cube;
473 assert( nVars <= ABC_ISOP_MAX_VAR );
474 Abc_TtClear( pRes, nWords );
475 Vec_IntForEachEntry( vCover, Cube, c )
476 {
477 Abc_TtFill( pCube, nWords );
478 for ( v = 0; v < nVars; v++ )
479 if ( ((Cube >> (v << 1)) & 3) == 1 )
480 Abc_TtSharp( pCube, pCube, pTtElems[v], nWords );
481 else if ( ((Cube >> (v << 1)) & 3) == 2 )
482 Abc_TtAnd( pCube, pCube, pTtElems[v], nWords, 0 );
483 if ( fXor )
484 Abc_TtXor( pRes, pRes, pCube, nWords, 0 );
485 else
486 Abc_TtOr( pRes, pRes, pCube, nWords );
487 }
488 if ( fCompl )
489 Abc_TtNot( pRes, nWords );
490}
Cube
struct cube Cube
Vec_IntForEachEntry
#define Vec_IntForEachEntry(vVec, Entry, i)
MACRO DEFINITIONS ///.
Definition vecInt.h:54

◆ Abc_IsopCheck()

word Abc_IsopCheck ( word * pOn,
word * pOnDc,
word * pRes,
int nVars,
word CostLim,
int * pCover )
extern

Definition at line 428 of file utilIsop.c.

429{
430 int nVarsNew; word Cost;
431 if ( nVars <= 6 )
432 return Abc_Isop6Cover( *pOn, *pOnDc, pRes, nVars, CostLim, pCover );
433 for ( nVarsNew = nVars; nVarsNew > 6; nVarsNew-- )
434 if ( Abc_TtHasVar( pOn, nVars, nVarsNew-1 ) || Abc_TtHasVar( pOnDc, nVars, nVarsNew-1 ) )
435 break;
436 if ( nVarsNew == 6 )
437 Cost = Abc_Isop6Cover( *pOn, *pOnDc, pRes, nVarsNew, CostLim, pCover );
438 else
439 Cost = s_pFuncIsopCover[nVarsNew]( pOn, pOnDc, pRes, CostLim, pCover );
440 Abc_TtStretch6( pRes, nVarsNew, nVars );
441 return Cost;
442}
Here is the call graph for this function:
Here is the caller graph for this function:

◆ Abc_IsopCnf()

int Abc_IsopCnf ( word * pFunc,
int nVars,
int nCubeLim,
int * pCover )

Function*************************************************************

Synopsis [Compute CNF assuming it does not exceed the limit.]

Description [Please note that pCover should have at least 32 extra entries!]

SideEffects []

SeeAlso []

Definition at line 562 of file utilIsop.c.

563{
564 word pRes[ABC_ISOP_MAX_WORD];
565 word Cost0, Cost1, CostInit = Abc_Cube2Cost(nCubeLim);
566 int c, nCubes0, nCubes1;
567 assert( nVars <= ABC_ISOP_MAX_VAR );
568 assert( Abc_TtHasVar( pFunc, nVars, nVars - 1 ) );
569 if ( nVars > 6 )
570 Cost0 = s_pFuncIsopCover[nVars]( pFunc, pFunc, pRes, CostInit, pCover );
571 else
572 Cost0 = Abc_Isop6Cover( *pFunc, *pFunc, pRes, nVars, CostInit, pCover );
573 if ( Cost0 >= CostInit )
574 return CostInit;
575 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
576 if ( nVars > 6 )
577 Cost1 = s_pFuncIsopCover[nVars]( pFunc, pFunc, pRes, CostInit, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
578 else
579 Cost1 = Abc_Isop6Cover( *pFunc, *pFunc, pRes, nVars, CostInit, pCover ? pCover + Abc_CostCubes(Cost0) : NULL );
580 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
581 if ( Cost0 + Cost1 >= CostInit )
582 return CostInit;
583 nCubes0 = Abc_CostCubes(Cost0);
584 nCubes1 = Abc_CostCubes(Cost1);
585 if ( pCover )
586 {
587 for ( c = 0; c < nCubes0; c++ )
588 pCover[c] |= (1 << Abc_Var2Lit(nVars, 0));
589 for ( c = 0; c < nCubes1; c++ )
590 pCover[c+nCubes0] |= (1 << Abc_Var2Lit(nVars, 1));
591 }
592 return nCubes0 + nCubes1;
593}
Here is the call graph for this function:

◆ Abc_IsopCountLits()

int Abc_IsopCountLits ( Vec_Int_t * vCover,
int nVars )

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 607 of file utilIsop.c.

608{
609 int i, k, Entry, Literal, nLits = 0;
610 if ( Vec_IntSize(vCover) == 0 || (Vec_IntSize(vCover) == 1 && Vec_IntEntry(vCover, 0) == 0) )
611 return 0;
612 Vec_IntForEachEntry( vCover, Entry, i )
613 {
614 for ( k = 0; k < nVars; k++ )
615 {
616 Literal = 3 & (Entry >> (k << 1));
617 if ( Literal == 1 ) // neg literal
618 nLits++;
619 else if ( Literal == 2 ) // pos literal
620 nLits++;
621 else if ( Literal != 0 )
622 assert( 0 );
623 }
624 }
625 return nLits;
626}
Here is the caller graph for this function:

◆ Abc_IsopNew()

word Abc_IsopNew ( word * pOn,
word * pOnDc,
word * pRes,
int nVars,
word CostLim,
int * pCover )

Definition at line 877 of file utilIsop.c.

878{
879 word pCube[ABC_ISOP_MAX_WORD];
880 word pOnset[ABC_ISOP_MAX_WORD];
881 word pOffset[ABC_ISOP_MAX_WORD];
882 int pBlocks[16], nBlocks, vTwo, uTwo;
883 int nWords = Abc_TtWordNum(nVars);
884 int c, v, u, iMint, Cube, nLits = 0;
885 assert( nVars <= ABC_ISOP_MAX_VAR );
886 Abc_TtClear( pRes, nWords );
887 Abc_TtCopy( pOnset, pOn, nWords, 0 );
888 Abc_TtCopy( pOffset, pOnDc, nWords, 1 );
889 if ( nVars < 6 )
890 pOnset[0] >>= (64 - (1 << nVars));
891 for ( c = 0; !Abc_TtIsConst0(pOnset, nWords); c++ )
892 {
893 // pick one minterm
894 iMint = Abc_TtFindFirstBit(pOnset, nVars);
895 for ( Cube = v = 0; v < nVars; v++ )
896 Cube |= (1 << Abc_Var2Lit(v, (iMint >> v) & 1));
897 // check expansion for the minterm
898 nBlocks = 0;
899 for ( v = 0; v < nVars; v++ )
900 if ( (pBlocks[v] = Abc_TtGetBit(pOffset, iMint ^ (1 << v))) )
901 nBlocks++;
902 // check second step
903 if ( nBlocks == nVars ) // cannot expand
904 {
905 Abc_TtSetBit( pRes, iMint );
906 Abc_TtXorBit( pOnset, iMint );
907 pCover[c] = Cube;
908 nLits += nVars;
909 continue;
910 }
911 // check dual expansion
912 vTwo = uTwo = -1;
913 if ( nBlocks < nVars - 1 )
914 {
915 for ( v = 0; v < nVars && vTwo == -1; v++ )
916 if ( !pBlocks[v] )
917 for ( u = v + 1; u < nVars; u++ )
918 if ( !pBlocks[u] )
919 {
920 if ( Abc_TtGetBit( pOffset, iMint ^ (1 << v) ^ (1 << u) ) )
921 continue;
922 // can expand both directions
923 vTwo = v;
924 uTwo = u;
925 break;
926 }
927 }
928 if ( vTwo == -1 ) // can expand only one
929 {
930 for ( v = 0; v < nVars; v++ )
931 if ( !pBlocks[v] )
932 break;
933 Abc_TtSetBit( pRes, iMint );
934 Abc_TtSetBit( pRes, iMint ^ (1 << v) );
935 Abc_TtXorBit( pOnset, iMint );
936 if ( Abc_TtGetBit(pOnset, iMint ^ (1 << v)) )
937 Abc_TtXorBit( pOnset, iMint ^ (1 << v) );
938 pCover[c] = Cube & ~(3 << Abc_Var2Lit(v, 0));
939 nLits += nVars - 1;
940 continue;
941 }
942 if ( nBlocks == nVars - 2 && vTwo >= 0 ) // can expand only these two
943 {
944 Abc_TtSetBit( pRes, iMint );
945 Abc_TtSetBit( pRes, iMint ^ (1 << vTwo) );
946 Abc_TtSetBit( pRes, iMint ^ (1 << uTwo) );
947 Abc_TtSetBit( pRes, iMint ^ (1 << vTwo) ^ (1 << uTwo) );
948 Abc_TtXorBit( pOnset, iMint );
949 if ( Abc_TtGetBit(pOnset, iMint ^ (1 << vTwo)) )
950 Abc_TtXorBit( pOnset, iMint ^ (1 << vTwo) );
951 if ( Abc_TtGetBit(pOnset, iMint ^ (1 << uTwo)) )
952 Abc_TtXorBit( pOnset, iMint ^ (1 << uTwo) );
953 if ( Abc_TtGetBit(pOnset, iMint ^ (1 << vTwo) ^ (1 << uTwo)) )
954 Abc_TtXorBit( pOnset, iMint ^ (1 << vTwo) ^ (1 << uTwo) );
955 pCover[c] = Cube & ~(3 << Abc_Var2Lit(vTwo, 0)) & ~(3 << Abc_Var2Lit(uTwo, 0));
956 nLits += nVars - 2;
957 continue;
958 }
959 // can expand others as well
960 Abc_TtClear( pCube, nWords );
961 Abc_TtSetBit( pCube, iMint );
962 Abc_TtSetBit( pCube, iMint ^ (1 << vTwo) );
963 Abc_TtSetBit( pCube, iMint ^ (1 << uTwo) );
964 Abc_TtSetBit( pCube, iMint ^ (1 << vTwo) ^ (1 << uTwo) );
965 Cube &= ~(3 << Abc_Var2Lit(vTwo, 0)) & ~(3 << Abc_Var2Lit(uTwo, 0));
966 assert( !Abc_TtIntersect2(pCube, pOffset, nWords) );
967 // expand against offset
968 for ( v = 0; v < nVars; v++ )
969 if ( v != vTwo && v != uTwo )
970 {
971 int Shift = Abc_Var2Lit( v, 0 );
972 if ( (Cube >> Shift) == 2 && Abc_TtCheckWithCubePos2Neg(pOffset, pCube, nWords, v) ) // pos literal
973 {
974 Abc_TtExpandCubePos2Neg( pCube, nWords, v );
975 Cube &= ~(3 << Shift);
976 }
977 else if ( (Cube >> Shift) == 1 && Abc_TtCheckWithCubeNeg2Pos(pOffset, pCube, nWords, v) ) // neg literal
978 {
979 Abc_TtExpandCubeNeg2Pos( pCube, nWords, v );
980 Cube &= ~(3 << Shift);
981 }
982 else
983 nLits++;
984 }
985 // add cube to solution
986 Abc_TtOr( pRes, pRes, pCube, nWords );
987 Abc_TtSharp( pOnset, pOnset, pCube, nWords );
988 pCover[c] = Cube;
989 }
990 pRes[0] = Abc_Tt6Stretch( pRes[0], nVars );
991 return Abc_Cube2Cost(c) | nLits;
992}

◆ Abc_IsopPrint()

void Abc_IsopPrint ( word * t,
int nVars,
Vec_Int_t * vCover,
int fTryBoth )

Definition at line 651 of file utilIsop.c.

652{
653 int fCompl = Abc_Isop( t, nVars, ABC_ISOP_MAX_CUBE, vCover, fTryBoth );
654 Abc_IsopPrintCover( vCover, nVars, fCompl );
655}
ABC_ISOP_MAX_CUBE
#define ABC_ISOP_MAX_CUBE
Definition utilIsop.c:37
Abc_Isop
int Abc_Isop(word *pFunc, int nVars, int nCubeLim, Vec_Int_t *vCover, int fTryBoth)
Definition utilIsop.c:511
Abc_IsopPrintCover
void Abc_IsopPrintCover(Vec_Int_t *vCover, int nVars, int fCompl)
Definition utilIsop.c:627
Here is the call graph for this function:

◆ Abc_IsopPrintCover()

void Abc_IsopPrintCover ( Vec_Int_t * vCover,
int nVars,
int fCompl )

Definition at line 627 of file utilIsop.c.

628{
629 int i, k, Entry, Literal;
630 if ( Vec_IntSize(vCover) == 0 || (Vec_IntSize(vCover) == 1 && Vec_IntEntry(vCover, 0) == 0) )
631 {
632 printf( "Constant %d\n", Vec_IntSize(vCover) );
633 return;
634 }
635 Vec_IntForEachEntry( vCover, Entry, i )
636 {
637 for ( k = 0; k < nVars; k++ )
638 {
639 Literal = 3 & (Entry >> (k << 1));
640 if ( Literal == 1 ) // neg literal
641 printf( "0" );
642 else if ( Literal == 2 ) // pos literal
643 printf( "1" );
644 else if ( Literal == 0 )
645 printf( "-" );
646 else assert( 0 );
647 }
648 printf( " %d\n", !fCompl );
649 }
650}
Here is the caller graph for this function:

◆ Abc_IsopTest()

int Abc_IsopTest ( word * pFunc,
int nVars,
Vec_Int_t * vCover )

Function*************************************************************

Synopsis [Compute CNF assuming it does not exceed the limit.]

Description [Please note that pCover should have at least 32 extra entries!]

SideEffects []

SeeAlso []

Definition at line 1022 of file utilIsop.c.

1023{
1024 int fVerbose = 0;
1025 static word TotalCost[6] = {0};
1026 static abctime TotalTime[6] = {0};
1027 static int Counter;
1028 word pRes[ABC_ISOP_MAX_WORD];
1029 word Cost;
1030 abctime clk;
1031 Counter++;
1032 if ( Counter == 9999 )
1033 {
1034 Abc_PrintTime( 1, "0", TotalTime[0] );
1035 Abc_PrintTime( 1, "1", TotalTime[1] );
1036 Abc_PrintTime( 1, "2", TotalTime[2] );
1037 Abc_PrintTime( 1, "3", TotalTime[3] );
1038 Abc_PrintTime( 1, "4", TotalTime[4] );
1039 Abc_PrintTime( 1, "5", TotalTime[5] );
1040 }
1041 assert( nVars <= ABC_ISOP_MAX_VAR );
1042// if ( fVerbose )
1043// Dau_DsdPrintFromTruth( pFunc, nVars ), printf( " " );
1044
1045 clk = Abc_Clock();
1046 Cost = Abc_IsopCheck( pFunc, pFunc, pRes, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1047 vCover->nSize = Abc_CostCubes(Cost);
1048 assert( vCover->nSize <= vCover->nCap );
1049 if ( fVerbose )
1050 printf( "%5d %7d ", Abc_CostCubes(Cost), Abc_CostLits(Cost) );
1051// Abc_IsopVerify( pFunc, nVars, pRes, vCover, 0, 0 );
1052 TotalCost[0] += Abc_CostCubes(Cost);
1053 TotalTime[0] += Abc_Clock() - clk;
1054
1055
1056 clk = Abc_Clock();
1057 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
1058 Cost = Abc_IsopCheck( pFunc, pFunc, pRes, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1059 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
1060 vCover->nSize = Abc_CostCubes(Cost);
1061 assert( vCover->nSize <= vCover->nCap );
1062 if ( fVerbose )
1063 printf( "%5d %7d ", Abc_CostCubes(Cost), Abc_CostLits(Cost) );
1064// Abc_IsopVerify( pFunc, nVars, pRes, vCover, 0, 1 );
1065 TotalCost[1] += Abc_CostCubes(Cost);
1066 TotalTime[1] += Abc_Clock() - clk;
1067
1068/*
1069 clk = Abc_Clock();
1070 Cost = Abc_EsopCheck( pFunc, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1071 vCover->nSize = Abc_CostCubes(Cost);
1072 assert( vCover->nSize <= vCover->nCap );
1073 if ( fVerbose )
1074 printf( "%5d %7d ", Abc_CostCubes(Cost), Abc_CostLits(Cost) );
1075// Abc_IsopVerify( pFunc, nVars, pRes, vCover, 1, 0 );
1076 TotalCost[2] += Abc_CostCubes(Cost);
1077 TotalTime[2] += Abc_Clock() - clk;
1078
1079
1080 clk = Abc_Clock();
1081 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
1082 Cost = Abc_EsopCheck( pFunc, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1083 Abc_TtNot( pFunc, Abc_TtWordNum(nVars) );
1084 vCover->nSize = Abc_CostCubes(Cost);
1085 assert( vCover->nSize <= vCover->nCap );
1086 if ( fVerbose )
1087 printf( "%5d %7d ", Abc_CostCubes(Cost), Abc_CostLits(Cost) );
1088// Abc_IsopVerify( pFunc, nVars, pRes, vCover, 1, 1 );
1089 TotalCost[3] += Abc_CostCubes(Cost);
1090 TotalTime[3] += Abc_Clock() - clk;
1091*/
1092
1093/*
1094 // try new computation
1095 clk = Abc_Clock();
1096 Cost = Abc_IsopNew( pFunc, pFunc, pRes, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1097 vCover->nSize = Abc_CostCubes(Cost);
1098 assert( vCover->nSize <= vCover->nCap );
1099 if ( fVerbose )
1100 printf( "%5d %7d ", Abc_CostCubes(Cost), Abc_CostLits(Cost) );
1101 Abc_IsopVerify( pFunc, nVars, pRes, vCover, 0, 0 );
1102 TotalCost[4] += Abc_CostCubes(Cost);
1103 TotalTime[4] += Abc_Clock() - clk;
1104*/
1105/*
1106 // try old computation
1107 clk = Abc_Clock();
1108 Cost = Kit_TruthIsop( (unsigned *)pFunc, nVars, vCover, 1 );
1109 vCover->nSize = Vec_IntSize(vCover);
1110 assert( vCover->nSize <= vCover->nCap );
1111 if ( fVerbose )
1112 printf( "%5d %7d ", Vec_IntSize(vCover), Abc_IsopCountLits(vCover, nVars) );
1113 TotalCost[4] += Vec_IntSize(vCover);
1114 TotalTime[4] += Abc_Clock() - clk;
1115*/
1116
1117 clk = Abc_Clock();
1118 Cost = Abc_Isop( pFunc, nVars, ABC_ISOP_MAX_CUBE, vCover, 1 );
1119 if ( fVerbose )
1120 printf( "%5d %7d ", Vec_IntSize(vCover), Abc_IsopCountLits(vCover, nVars) );
1121 TotalCost[5] += Vec_IntSize(vCover);
1122 TotalTime[5] += Abc_Clock() - clk;
1123
1124 if ( fVerbose )
1125 printf( " | %8d %8d %8d %8d %8d %8d", (int)TotalCost[0], (int)TotalCost[1], (int)TotalCost[2], (int)TotalCost[3], (int)TotalCost[4], (int)TotalCost[5] );
1126 if ( fVerbose )
1127 printf( "\n" );
1128//Abc_IsopPrintCover( vCover, nVars, 0 );
1129 return 1;
1130}
abctime
ABC_INT64_T abctime
Definition abc_global.h:332
Abc_IsopCountLits
int Abc_IsopCountLits(Vec_Int_t *vCover, int nVars)
Definition utilIsop.c:607
Here is the call graph for this function:

◆ Abc_IsopTestNew()

void Abc_IsopTestNew ( )

Definition at line 993 of file utilIsop.c.

994{
995 int nVars = 4;
996 Vec_Int_t * vCover = Vec_IntAlloc( 1000 );
997 word r, t = (s_Truths6[0] & s_Truths6[1]) ^ (s_Truths6[2] & s_Truths6[3]), copy = t;
998// word r, t = ~s_Truths6[0] | (s_Truths6[1] & s_Truths6[2] & s_Truths6[3]), copy = t;
999// word r, t = 0xABCDABCDABCDABCD, copy = t;
1000// word r, t = 0x6996000000006996, copy = t;
1001// word Cost = Abc_IsopNew( &t, &t, &r, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1002 word Cost = Abc_EsopCheck( &t, nVars, Abc_Cube2Cost(ABC_ISOP_MAX_CUBE), Vec_IntArray(vCover) );
1003 vCover->nSize = Abc_CostCubes(Cost);
1004 assert( vCover->nSize <= vCover->nCap );
1005 printf( "Cubes = %d. Lits = %d.\n", Abc_CostCubes(Cost), Abc_CostLits(Cost) );
1006 Abc_IsopPrintCover( vCover, nVars, 0 );
1007 Abc_IsopVerify( &copy, nVars, &r, vCover, 1, 0 );
1008 Vec_IntFree( vCover );
1009}
Vec_Int_t
typedefABC_NAMESPACE_IMPL_START struct Vec_Int_t_ Vec_Int_t
DECLARATIONS ///.
Definition bblif.c:37
Here is the call graph for this function: