cswTable.c File Reference

#include "cswInt.h"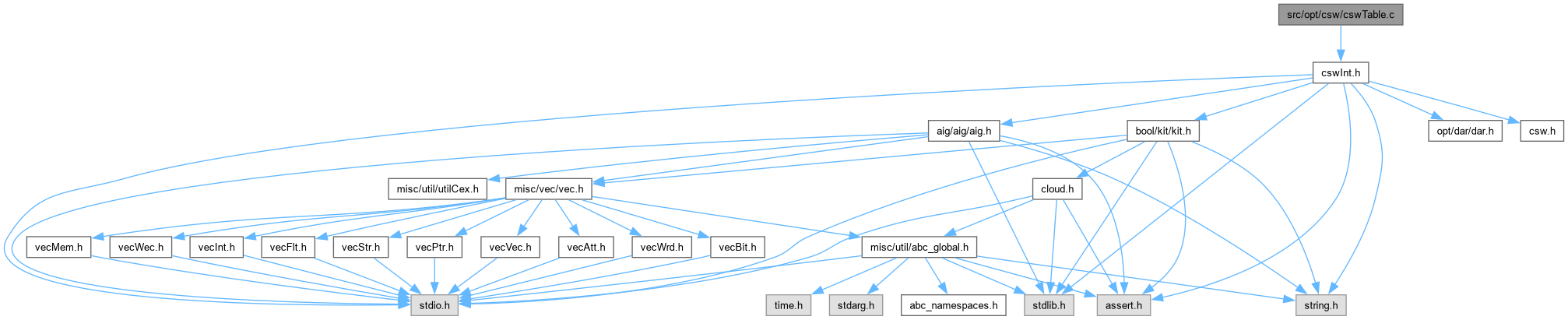

Include dependency graph for cswTable.c:

Go to the source code of this file.

Functions
ABC_NAMESPACE_IMPL_START unsigned	Csw_CutHash (Csw_Cut_t *pCut)
	DECLARATIONS ///.
int	Csw_TableCountCuts (Csw_Man_t *p)
void	Csw_TableCutInsert (Csw_Man_t *p, Csw_Cut_t *pCut)
Aig_Obj_t *	Csw_TableCutLookup (Csw_Man_t *p, Csw_Cut_t *pCut)

Function Documentation

Csw_CutHash()

ABC_NAMESPACE_IMPL_START unsigned Csw_CutHash

(

Csw_Cut_t *

pCut

)

DECLARATIONS ///.

CFile****************************************************************

FileName [cswTable.c]

SystemName [ABC: Logic synthesis and verification system.]

PackageName [Cut sweeping.]

Synopsis []

Author [Alan Mishchenko]

Affiliation [UC Berkeley]

Date [Ver. 1.0. Started - July 11, 2007.]

Revision [

Id

cswTable.c,v 1.00 2007/07/11 00:00:00 alanmi Exp

] FUNCTION DEFINITIONS /// Function*************************************************************

Synopsis [Computes hash value of the cut.]

Description []

SideEffects []

SeeAlso []

Definition at line 45 of file cswTable.c.

{
    static int s_FPrimes[128] = { 
        1009, 1049, 1093, 1151, 1201, 1249, 1297, 1361, 1427, 1459, 
        1499, 1559, 1607, 1657, 1709, 1759, 1823, 1877, 1933, 1997, 
        2039, 2089, 2141, 2213, 2269, 2311, 2371, 2411, 2467, 2543, 
        2609, 2663, 2699, 2741, 2797, 2851, 2909, 2969, 3037, 3089, 
        3169, 3221, 3299, 3331, 3389, 3461, 3517, 3557, 3613, 3671, 
        3719, 3779, 3847, 3907, 3943, 4013, 4073, 4129, 4201, 4243, 
        4289, 4363, 4441, 4493, 4549, 4621, 4663, 4729, 4793, 4871, 
        4933, 4973, 5021, 5087, 5153, 5227, 5281, 5351, 5417, 5471, 
        5519, 5573, 5651, 5693, 5749, 5821, 5861, 5923, 6011, 6073, 
        6131, 6199, 6257, 6301, 6353, 6397, 6481, 6563, 6619, 6689, 
        6737, 6803, 6863, 6917, 6977, 7027, 7109, 7187, 7237, 7309, 
        7393, 7477, 7523, 7561, 7607, 7681, 7727, 7817, 7877, 7933, 
        8011, 8039, 8059, 8081, 8093, 8111, 8123, 8147
    };
    unsigned uHash;
    int i;
    assert( pCut->nFanins <= 16 );
    uHash = 0;
    for ( i = 0; i < pCut->nFanins; i++ )
        uHash ^= pCut->pFanins[i] * s_FPrimes[i];
    return uHash;
}

Here is the caller graph for this function:

Csw_TableCountCuts()

int Csw_TableCountCuts

(

Csw_Man_t *

p

)

Function*************************************************************

Synopsis [Returns the total number of cuts in the table.]

Description []

SideEffects []

SeeAlso []

Definition at line 82 of file cswTable.c.

{
    Csw_Cut_t * pEnt;
    int i, Counter = 0;
    for ( i = 0; i < p->nTableSize; i++ )
        for ( pEnt = p->pTable[i]; pEnt; pEnt = pEnt->pNext )
            Counter++;
    return Counter;
}

Here is the caller graph for this function:

Csw_TableCutInsert()

void Csw_TableCutInsert	(	Csw_Man_t *	p,
		Csw_Cut_t *	pCut )

Function*************************************************************

Synopsis [Adds the cut to the hash table.]

Description []

SideEffects []

SeeAlso []

Definition at line 103 of file cswTable.c.

{
    int iEntry = Csw_CutHash(pCut) % p->nTableSize;
    pCut->pNext = p->pTable[iEntry];
    p->pTable[iEntry] = pCut;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Csw_TableCutLookup()

Aig_Obj_t * Csw_TableCutLookup	(	Csw_Man_t *	p,
		Csw_Cut_t *	pCut )

Function*************************************************************

Synopsis [Returns an equivalent node if it exists.]

Description []

SideEffects []

SeeAlso []

Definition at line 121 of file cswTable.c.

{
    Aig_Obj_t * pRes = NULL;
    Csw_Cut_t * pEnt;
    unsigned * pTruthNew, * pTruthOld;
    int iEntry = Csw_CutHash(pCut) % p->nTableSize;
    for ( pEnt = p->pTable[iEntry]; pEnt; pEnt = pEnt->pNext )
    {
        if ( pEnt->nFanins != pCut->nFanins )
            continue;
        if ( pEnt->uSign != pCut->uSign )
            continue;
        if ( memcmp( pEnt->pFanins, pCut->pFanins, sizeof(int) * pCut->nFanins ) )
            continue;
        pTruthOld = Csw_CutTruth(pEnt);
        pTruthNew = Csw_CutTruth(pCut);
        if ( (pTruthOld[0] & 1) == (pTruthNew[0] & 1) )
        {
            if ( Kit_TruthIsEqual( pTruthOld, pTruthNew, pCut->nFanins ) )
            {
                pRes = Aig_ManObj( p->pManRes, pEnt->iNode );
                assert( pRes->fPhase == Aig_ManObj( p->pManRes, pCut->iNode )->fPhase );
                break;
            }
        }
        else
        {
            if ( Kit_TruthIsOpposite( pTruthOld, pTruthNew, pCut->nFanins ) )
            {
                pRes = Aig_Not( Aig_ManObj( p->pManRes, pEnt->iNode ) );
                assert( Aig_Regular(pRes)->fPhase != Aig_ManObj( p->pManRes, pCut->iNode )->fPhase );
                break;
            }
        }
    }
    return pRes;
}

Here is the call graph for this function:

Here is the caller graph for this function: