unate.c File Reference

#include "espresso.h"

Include dependency graph for unate.c:

Go to the source code of this file.

Macros
#define	MAGIC   500 /* save 500 cubes before containment */

Functions
pcover	map_cover_to_unate (pcube *T)
pcover	map_unate_to_cover (pset_family A)
pset_family	unate_compl (pset_family A)
pset_family	unate_complement (pset_family A)
pset_family	exact_minimum_cover (IN pset_family T)
pset_family	unate_intersect (pset_family A, pset_family B, bool largest_only)

Macro Definition Documentation

MAGIC

#define MAGIC   500 /* save 500 cubes before containment */

Definition at line 303 of file unate.c.

Function Documentation

exact_minimum_cover()

pset_family exact_minimum_cover

(

IN pset_family

T

)

Definition at line 226 of file unate.c.

{
    register pset p, last, p1;
    register int i, n;
    int lev, lvl;
    pset nlast;
    pset_family temp;
    long start = ptime();
    struct {
    pset_family sf;
    int level;
    } stack[32];                /* 32 suffices for 2 ** 32 cubes ! */
 
    if (T->count <= 0)
    return sf_new(1, T->sf_size);
    for(n = T->count, lev = 0; n != 0; n >>= 1, lev++)   ;
 
    /* A simple heuristic ordering */
    T = lex_sort(sf_save(T));
 
    /* Push a full set on the stack to get things started */
    n = 1;
    stack[0].sf = sf_new(1, T->sf_size);
    stack[0].level = lev;
    set_fill(GETSET(stack[0].sf, stack[0].sf->count++), T->sf_size);
 
    nlast = GETSET(T, T->count - 1);
    foreach_set(T, last, p) {
 
    /* "unstack" the set into a family */
    temp = sf_new(set_ord(p), T->sf_size);
    for(i = 0; i < T->sf_size; i++)
        if (is_in_set(p, i)) {
        p1 = set_fill(GETSET(temp, temp->count++), T->sf_size);
        set_remove(p1, i);
        }
    stack[n].sf = temp;
    stack[n++].level = lev;
 
    /* Pop the stack and perform (leveled) intersections */
    while (n > 1 && (stack[n-1].level==stack[n-2].level || p == nlast)) {
        temp = unate_intersect(stack[n-1].sf, stack[n-2].sf, FALSE);
        lvl = MIN(stack[n-1].level, stack[n-2].level) - 1;
        if (debug & MINCOV && lvl < 10) {
        printf("# EXACT_MINCOV[%d]: %4d = %4d x %4d, time = %s\n",
            lvl, temp->count, stack[n-1].sf->count,
            stack[n-2].sf->count, print_time(ptime() - start));
        (void) fflush(stdout);
        }
        sf_free(stack[n-2].sf);
        sf_free(stack[n-1].sf);
        stack[n-2].sf = temp;
        stack[n-2].level = lvl;
        n--;
    }
    }
 
    temp = stack[0].sf;
    p1 = set_fill(set_new(T->sf_size), T->sf_size);
    foreach_set(temp, last, p)
    INLINEset_diff(p, p1, p);
    set_free(p1);
    if (debug & MINCOV1) {
    printf("MINCOV: family of all minimal coverings is\n");
    sf_print(temp);
    }
    sf_free(T);         /* this is the copy of T we made ... */
    return temp;
}

Here is the call graph for this function:

map_cover_to_unate()

pcover map_cover_to_unate

(

pcube *

T

)

Definition at line 23 of file unate.c.

{
    register unsigned int word_test, word_set, bit_test, bit_set;
    register pcube p, pA;
    pset_family A;
    pcube *T1;
    int ncol, i;
 
    A = sf_new(CUBELISTSIZE(T), cdata.vars_unate);
    A->count = CUBELISTSIZE(T);
    foreachi_set(A, i, p) {
    (void) set_clear(p, A->sf_size);
    }
    ncol = 0;
 
    for(i = 0; i < cube.size; i++) {
    if (cdata.part_zeros[i] > 0) {
        assert(ncol <= cdata.vars_unate);
 
        /* Copy a column from T to A */
        word_test = WHICH_WORD(i);
        bit_test = 1 << WHICH_BIT(i);
        word_set = WHICH_WORD(ncol);
        bit_set = 1 << WHICH_BIT(ncol);
 
        pA = A->data;
        for(T1 = T+2; (p = *T1++) != 0; ) {
        if ((p[word_test] & bit_test) == 0) {
            pA[word_set] |= bit_set;
        }
        pA += A->wsize;
        }
 
        ncol++;
    }
    }
 
    return A;
}

Here is the call graph for this function:

map_unate_to_cover()

pcover map_unate_to_cover

(

pset_family

A

)

Definition at line 64 of file unate.c.

{
    register int i, ncol, lp;
    register pcube p, pB;
    int var, nunate, *unate;
    pcube last;
    pset_family B;
 
    B = sf_new(A->count, cube.size);
    B->count = A->count;
 
    /* Find the unate variables */
    unate = ALLOC(int, cube.num_vars);
    nunate = 0;
    for(var = 0; var < cube.num_vars; var++) {
    if (cdata.is_unate[var]) {
        unate[nunate++] = var;
    }
    }
 
    /* Loop for each set of A */
    pB = B->data;
    foreach_set(A, last, p) {
 
    /* Initialize this set of B */
    INLINEset_fill(pB, cube.size);
 
    /* Now loop for the unate variables; if the part is in A,
     * then this variable of B should be a single 1 in the unate
     * part.
     */
    for(ncol = 0; ncol < nunate; ncol++) {
        if (is_in_set(p, ncol)) {
        lp = cube.last_part[unate[ncol]];
        for(i = cube.first_part[unate[ncol]]; i <= lp; i++) {
            if (cdata.part_zeros[i] == 0) {
            set_remove(pB, i);
            }
        }
        }
    }
    pB += B->wsize;
    }
 
    FREE(unate);
    return B;
}

Here is the call graph for this function:

unate_compl()

pset_family unate_compl

(

pset_family

A

)

Definition at line 117 of file unate.c.

{
    register pset p, last;
 
    /* Make sure A is single-cube containment minimal */
/*    A = sf_rev_contain(A);*/
 
    foreach_set(A, last, p) {
    PUTSIZE(p, set_ord(p));
    }
 
    /* Recursively find the complement */
    A = unate_complement(A);
 
    /* Now, we can guarantee a minimal result by containing the result */
    A = sf_rev_contain(A);
    return A;
}

Here is the call graph for this function:

unate_complement()

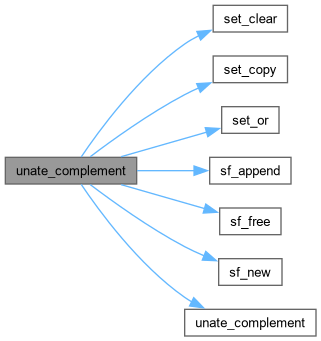
pset_family unate_complement

(

pset_family

A

)

Definition at line 141 of file unate.c.

{
    pset_family Abar;
    register pset p, p1, restrict;
    register int i;
    int max_i, min_set_ord, j;
 
    /* Check for no sets in the matrix -- complement is the universe */
    if (A->count == 0) {
    sf_free(A);
    Abar = sf_new(1, A->sf_size);
    (void) set_clear(GETSET(Abar, Abar->count++), A->sf_size);
 
    /* Check for a single set in the maxtrix -- compute de Morgan complement */
    } else if (A->count == 1) {
    p = A->data;
    Abar = sf_new(A->sf_size, A->sf_size);
    for(i = 0; i < A->sf_size; i++) {
        if (is_in_set(p, i)) {
        p1 = set_clear(GETSET(Abar, Abar->count++), A->sf_size);
        set_insert(p1, i);
        }
    }
    sf_free(A);
 
    } else {
 
    /* Select splitting variable as the variable which belongs to a set
     * of the smallest size, and which has greatest column count
     */
    restrict = set_new(A->sf_size);
    min_set_ord = A->sf_size + 1;
    foreachi_set(A, i, p) {
        if (SIZE(p) < min_set_ord) {
        set_copy(restrict, p);
        min_set_ord = SIZE(p);
        } else if (SIZE(p) == min_set_ord) {
        set_or(restrict, restrict, p);
        }
    }
 
    /* Check for no data (shouldn't happen ?) */
    if (min_set_ord == 0) {
        A->count = 0;
        Abar = A;
 
    /* Check for "essential" columns */
    } else if (min_set_ord == 1) {
        Abar = unate_complement(abs_covered_many(A, restrict));
        sf_free(A);
        foreachi_set(Abar, i, p) {
        set_or(p, p, restrict);
        }
 
    /* else, recur as usual */
    } else {
        max_i = abs_select_restricted(A, restrict);
 
        /* Select those rows of A which are not covered by max_i,
         * recursively find all minimal covers of these rows, and
         * then add back in max_i
         */
        Abar = unate_complement(abs_covered(A, max_i));
        foreachi_set(Abar, i, p) {
        set_insert(p, max_i);
        }
 
        /* Now recur on A with all zero's on column max_i */
        foreachi_set(A, i, p) {
        if (is_in_set(p, max_i)) {
            set_remove(p, max_i);
            j = SIZE(p) - 1;
            PUTSIZE(p, j);
        }
        }
 
        Abar = sf_append(Abar, unate_complement(A));
    }
    set_free(restrict);
    }
 
    return Abar;
}

Here is the call graph for this function:

unate_intersect()

pset_family unate_intersect	(	pset_family	A,
		pset_family	B,
		bool	largest_only )

Definition at line 305 of file unate.c.

{
    register pset pi, pj, lasti, lastj, pt;
    pset_family T, Tsave;
    bool save;
    int maxord, ord;
 
    /* How large should each temporary result cover be ? */
    T = sf_new(MAGIC, A->sf_size);
    Tsave = NULL;
    maxord = 0;
    pt = T->data;
 
    /* Form pairwise intersection of each set of A with each cube of B */
    foreach_set(A, lasti, pi) {
 
    foreach_set(B, lastj, pj) {
 
        save = set_andp(pt, pi, pj);
 
        /* Check if we want the largest only */
        if (save && largest_only) {
        if ((ord = set_ord(pt)) > maxord) {
            /* discard Tsave and T */
            if (Tsave != NULL) {
            sf_free(Tsave);
            Tsave = NULL;
            }
            pt = T->data;
            T->count = 0;
            /* Re-create pt (which was just thrown away) */
            (void) set_and(pt, pi, pj);
            maxord = ord;
        } else if (ord < maxord) {
            save = FALSE;
        }
        }
 
        if (save) {
        if (++T->count >= T->capacity) {
            T = sf_contain(T);
            Tsave = (Tsave == NULL) ? T : sf_union(Tsave, T);
            T = sf_new(MAGIC, A->sf_size);
            pt = T->data;
        } else {
            pt += T->wsize;
        }
        }
    }
    }
 
 
    /* Contain the final result and merge it into Tsave */
    T = sf_contain(T);
    Tsave = (Tsave == NULL) ? T : sf_union(Tsave, T);
 
    return Tsave;
}

Here is the call graph for this function: