sbdWin.c File Reference

#include "sbdInt.h"

Include dependency graph for sbdWin.c:

Go to the source code of this file.

Functions
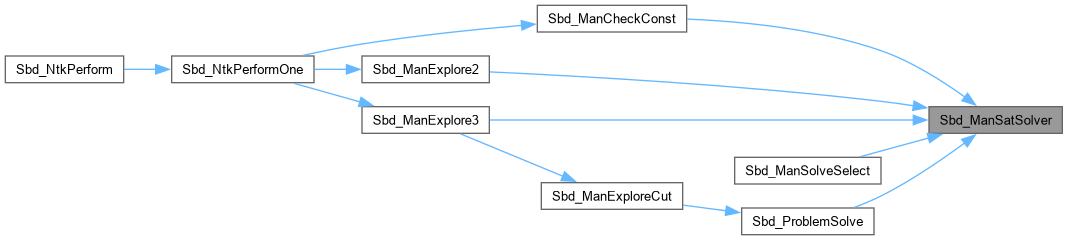
ABC_NAMESPACE_IMPL_START sat_solver *	Sbd_ManSatSolver (sat_solver *pSat, Gia_Man_t *p, Vec_Int_t *vMirrors, int Pivot, Vec_Int_t *vWinObjs, Vec_Int_t *vObj2Var, Vec_Int_t *vTfo, Vec_Int_t *vRoots, int fQbf)
	DECLARATIONS ///.
word	Sbd_ManSolve (sat_solver *pSat, int PivotVar, int FreeVar, Vec_Int_t *vDivSet, Vec_Int_t *vDivVars, Vec_Int_t *vDivValues, Vec_Int_t *vTemp)
int	Sbd_ManSolve2 (sat_solver *pSat, int PivotVar, int FreeVar, Vec_Int_t *vDivVars, Vec_Int_t *vDivValues, Vec_Int_t *vTemp, Vec_Int_t *vSop)
word	Sbd_ManSolverSupp (Vec_Int_t *vSop, int *pInds, int *pnVars)
void	Sbd_ManSolverPrint (Vec_Int_t *vSop)
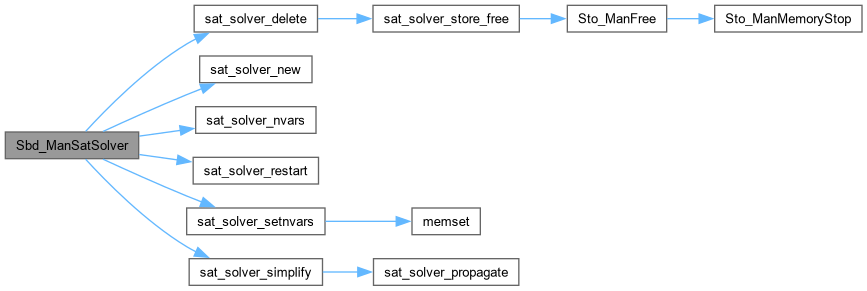
void	Sbd_ManSolveSelect (Gia_Man_t *p, Vec_Int_t *vMirrors, int Pivot, Vec_Int_t *vDivVars, Vec_Int_t *vDivValues, Vec_Int_t *vWinObjs, Vec_Int_t *vObj2Var, Vec_Int_t *vTfo, Vec_Int_t *vRoots)
int	Sbd_ManCollectConstants (sat_solver *pSat, int nCareMints[2], int PivotVar, word *pVarSims[], Vec_Int_t *vInds)
int	Sbd_ManCollectConstantsNew (sat_solver *pSat, Vec_Int_t *vDivVars, int nConsts, int PivotVar, word *pOnset, word *pOffset)

Function Documentation

Sbd_ManCollectConstants()

int Sbd_ManCollectConstants	(	sat_solver *	pSat,
		int	nCareMints[2],
		int	PivotVar,
		word *	pVarSims[],
		Vec_Int_t *	vInds )

Definition at line 411 of file sbdWin.c.

{
    int nBTLimit = 0;
    int i, Ind; 
    assert( Vec_IntSize(vInds) == nCareMints[0] + nCareMints[1] );
    Vec_IntForEachEntry( vInds, Ind, i )
    {
        int fOffSet = (int)(i < nCareMints[0]);
        int status, k, iLit = Abc_Var2Lit( PivotVar, fOffSet );
        sat_solver_random_polarity( pSat );
        status = sat_solver_solve( pSat, &iLit, &iLit + 1, nBTLimit, 0, 0, 0 );
        if ( status == l_Undef )
            return -2;
        if ( status == l_False )
            return fOffSet;
        for ( k = 0; k <= PivotVar; k++ )
            if ( Abc_TtGetBit(pVarSims[k], Ind) != sat_solver_var_value(pSat, k) )
                Abc_TtXorBit(pVarSims[k], Ind);
    }
    return -1;
}

Here is the caller graph for this function:

Sbd_ManCollectConstantsNew()

int Sbd_ManCollectConstantsNew	(	sat_solver *	pSat,
		Vec_Int_t *	vDivVars,
		int	nConsts,
		int	PivotVar,
		word *	pOnset,
		word *	pOffset )

Definition at line 433 of file sbdWin.c.

{
    int nBTLimit = 0;
    int n, i, k, status, iLit, iVar; 
    word * pPats[2] = {pOnset, pOffset};
    assert( Vec_IntSize(vDivVars) < 64 );
    for ( n = 0; n < 2; n++ )
    for ( i = 0; i < nConsts; i++ )
    {
        sat_solver_random_polarity( pSat );
        iLit = Abc_Var2Lit( PivotVar, n );
        status = sat_solver_solve( pSat, &iLit, &iLit + 1, nBTLimit, 0, 0, 0 );
        if ( status == l_Undef )
            return -2;
        if ( status == l_False )
            return n;
        pPats[n][i] = ((word)!n) << Vec_IntSize(vDivVars);
        Vec_IntForEachEntry( vDivVars, iVar, k )
            if ( sat_solver_var_value(pSat, iVar) )
                Abc_TtXorBit(&pPats[n][i], k);
    }
    return -1;
}

Here is the caller graph for this function:

Sbd_ManSatSolver()

ABC_NAMESPACE_IMPL_START sat_solver * Sbd_ManSatSolver	(	sat_solver *	pSat,
		Gia_Man_t *	p,
		Vec_Int_t *	vMirrors,
		int	Pivot,
		Vec_Int_t *	vWinObjs,
		Vec_Int_t *	vObj2Var,
		Vec_Int_t *	vTfo,
		Vec_Int_t *	vRoots,
		int	fQbf )

DECLARATIONS ///.

CFile****************************************************************

FileName [sbd.c]

SystemName [ABC: Logic synthesis and verification system.]

PackageName [SAT-based optimization using internal don't-cares.]

Synopsis []

Author [Alan Mishchenko]

Affiliation [UC Berkeley]

Date [Ver. 1.0. Started - June 20, 2005.]

Revision [

Id

sbd.c,v 1.00 2005/06/20 00:00:00 alanmi Exp

] FUNCTION DEFINITIONS /// Function*************************************************************

Synopsis [Constructs SAT solver for the window.]

Description [The window for the pivot node (Pivot) is represented as a DFS ordered array of objects (vWinObjs) whose indexed in the array (which will be used as SAT variables) are given in array vObj2Var. The TFO nodes are listed as the last ones in vWinObjs. The root nodes are labeled with Abc_LitIsCompl() in vTfo and also given in vRoots. If fQbf is 1, returns the instance meant for QBF solving. It is using the last variable (LastVar) as the placeholder for the second copy of the pivot node.]

SideEffects []

SeeAlso []

Definition at line 52 of file sbdWin.c.

{
    Gia_Obj_t * pObj;
    int i, iLit = 1, iObj, Fan0, Fan1, Lit0m, Lit1m, Node, fCompl0, fCompl1, RetValue;
    int TfoStart = Vec_IntSize(vWinObjs) - Vec_IntSize(vTfo);
    int PivotVar = Vec_IntEntry(vObj2Var, Pivot);
    int LastVar = Vec_IntSize(vWinObjs) + Vec_IntSize(vTfo) + Vec_IntSize(vRoots);
    //Vec_IntPrint( vWinObjs );
    //Vec_IntPrint( vTfo );
    //Vec_IntPrint( vRoots );
    // create SAT solver
    if ( pSat == NULL )
        pSat = sat_solver_new();
    else
        sat_solver_restart( pSat );
    sat_solver_setnvars( pSat, Vec_IntSize(vWinObjs) + Vec_IntSize(vTfo) + Vec_IntSize(vRoots) + SBD_FVAR_MAX );
    // create constant 0 clause
    sat_solver_addclause( pSat, &iLit, &iLit + 1 );
    // add clauses for all nodes
    Vec_IntForEachEntryStart( vWinObjs, iObj, i, 1 )
    {
        pObj = Gia_ManObj( p, iObj );
        if ( Gia_ObjIsCi(pObj) )
            continue;
        assert( Gia_ObjIsAnd(pObj) );
        assert( Vec_IntEntry( vMirrors, iObj ) < 0 );
        Node = Vec_IntEntry( vObj2Var, iObj );
        Lit0m = Vec_IntEntry( vMirrors, Gia_ObjFaninId0(pObj, iObj) );
        Lit1m = Vec_IntEntry( vMirrors, Gia_ObjFaninId1(pObj, iObj) );
        Fan0 = Lit0m >= 0 ? Abc_Lit2Var(Lit0m) : Gia_ObjFaninId0(pObj, iObj);
        Fan1 = Lit1m >= 0 ? Abc_Lit2Var(Lit1m) : Gia_ObjFaninId1(pObj, iObj);
        Fan0 = Vec_IntEntry( vObj2Var, Fan0 );
        Fan1 = Vec_IntEntry( vObj2Var, Fan1 );
        fCompl0 = Gia_ObjFaninC0(pObj) ^ (Lit0m >= 0 && Abc_LitIsCompl(Lit0m));
        fCompl1 = Gia_ObjFaninC1(pObj) ^ (Lit1m >= 0 && Abc_LitIsCompl(Lit1m));
        if ( Gia_ObjIsXor(pObj) )
            sat_solver_add_xor( pSat, Node, Fan0, Fan1, fCompl0 ^ fCompl1 );
        else
            sat_solver_add_and( pSat, Node, Fan0, Fan1, fCompl0, fCompl1, 0 );
    }
    // add second clauses for the TFO
    Vec_IntForEachEntryStart( vWinObjs, iObj, i, TfoStart )
    {
        pObj = Gia_ManObj( p, iObj );
        assert( Gia_ObjIsAnd(pObj) );
        assert( Vec_IntEntry( vMirrors, iObj ) < 0 );
        Node = Vec_IntEntry( vObj2Var, iObj ) + Vec_IntSize(vTfo);
        Lit0m = Vec_IntEntry( vMirrors, Gia_ObjFaninId0(pObj, iObj) );
        Lit1m = Vec_IntEntry( vMirrors, Gia_ObjFaninId1(pObj, iObj) );
        Fan0 = Lit0m >= 0 ? Abc_Lit2Var(Lit0m) : Gia_ObjFaninId0(pObj, iObj);
        Fan1 = Lit1m >= 0 ? Abc_Lit2Var(Lit1m) : Gia_ObjFaninId1(pObj, iObj);
        Fan0 = Vec_IntEntry( vObj2Var, Fan0 );
        Fan1 = Vec_IntEntry( vObj2Var, Fan1 );
        Fan0 = Fan0 < TfoStart ? Fan0 : Fan0 + Vec_IntSize(vTfo);
        Fan1 = Fan1 < TfoStart ? Fan1 : Fan1 + Vec_IntSize(vTfo);
        if ( fQbf )
        {
            Fan0 = Fan0 == PivotVar ? LastVar : Fan0;
            Fan1 = Fan1 == PivotVar ? LastVar : Fan1;
        }
        fCompl0 = Gia_ObjFaninC0(pObj) ^ (!fQbf && Fan0 == PivotVar) ^ (Lit0m >= 0 && Abc_LitIsCompl(Lit0m));
        fCompl1 = Gia_ObjFaninC1(pObj) ^ (!fQbf && Fan1 == PivotVar) ^ (Lit1m >= 0 && Abc_LitIsCompl(Lit1m));
        if ( Gia_ObjIsXor(pObj) )
            sat_solver_add_xor( pSat, Node, Fan0, Fan1, fCompl0 ^ fCompl1 );
        else
            sat_solver_add_and( pSat, Node, Fan0, Fan1, fCompl0, fCompl1, 0 );
    }
    if ( Vec_IntSize(vRoots) > 0 )
    {
        // create XOR clauses for the roots
        int nVars = Vec_IntSize(vWinObjs) + Vec_IntSize(vTfo);
        Vec_Int_t * vFaninVars = Vec_IntAlloc( Vec_IntSize(vRoots) );
        Vec_IntForEachEntry( vRoots, iObj, i )
        {
            assert( Vec_IntEntry( vMirrors, iObj ) < 0 );
            Node = Vec_IntEntry( vObj2Var, iObj );
            Vec_IntPush( vFaninVars, Abc_Var2Lit(nVars, 0) );
            sat_solver_add_xor( pSat, Node, Node + Vec_IntSize(vTfo), nVars++, 0 );
        }
        // make OR clause for the last nRoots variables
        RetValue = sat_solver_addclause( pSat, Vec_IntArray(vFaninVars), Vec_IntLimit(vFaninVars) );
        Vec_IntFree( vFaninVars );
        if ( RetValue == 0 )
        {
            sat_solver_delete( pSat );
            return NULL;
        }
        assert( sat_solver_nvars(pSat) == nVars + SBD_FVAR_MAX );
    }
    else if ( fQbf )
    {
        int n, pLits[2];
        for ( n = 0; n < 2; n++ )
        {
            pLits[0] = Abc_Var2Lit( PivotVar, n );
            pLits[1] = Abc_Var2Lit( LastVar, n );
            RetValue = sat_solver_addclause( pSat, pLits, pLits + 2 );
            assert( RetValue );
        }
    }
    // finalize
    RetValue = sat_solver_simplify( pSat );
    if ( RetValue == 0 )
    {
        sat_solver_delete( pSat );
        return NULL;    
    }
    return pSat;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Sbd_ManSolve()

word Sbd_ManSolve	(	sat_solver *	pSat,
		int	PivotVar,
		int	FreeVar,
		Vec_Int_t *	vDivSet,
		Vec_Int_t *	vDivVars,
		Vec_Int_t *	vDivValues,
		Vec_Int_t *	vTemp )

Function*************************************************************

Synopsis [Solves one SAT problem.]

Description [Computes node function for PivotVar with fanins in vDivSet using don't-care represented in the SAT solver. Uses array vValues to return the values of the first Vec_IntSize(vValues) SAT variables in case the implementation of the node with the given fanins does not exist.]

SideEffects []

SeeAlso []

Definition at line 178 of file sbdWin.c.

{
    int nBTLimit = 0;
    word uCube, uTruth = 0;
    int status, i, iVar, nFinal, * pFinal, pLits[2], nIter = 0;
    assert( FreeVar < sat_solver_nvars(pSat) );
    assert( Vec_IntSize(vDivVars) == Vec_IntSize(vDivValues) );
    pLits[0] = Abc_Var2Lit( PivotVar, 0 ); // F = 1
    pLits[1] = Abc_Var2Lit( FreeVar, 0 );  // iNewLit
    while ( 1 ) 
    {
        // find onset minterm
        status = sat_solver_solve( pSat, pLits, pLits + 2, nBTLimit, 0, 0, 0 );
        if ( status == l_Undef )
            return SBD_SAT_UNDEC;
        if ( status == l_False )
            return uTruth;
        assert( status == l_True );
        // remember variable values
        Vec_IntForEachEntry( vDivVars, iVar, i )
            Vec_IntWriteEntry( vDivValues, i, 2*sat_solver_var_value(pSat, iVar) );
        // collect divisor literals
        Vec_IntClear( vTemp );
        Vec_IntPush( vTemp, Abc_LitNot(pLits[0]) ); // F = 0
        Vec_IntForEachEntry( vDivSet, iVar, i )
            Vec_IntPush( vTemp, sat_solver_var_literal(pSat, iVar) );
        // check against offset
        status = sat_solver_solve( pSat, Vec_IntArray(vTemp), Vec_IntArray(vTemp) + Vec_IntSize(vTemp), nBTLimit, 0, 0, 0 );
        if ( status == l_Undef )
            return SBD_SAT_UNDEC;
        if ( status == l_True )
            break;
        assert( status == l_False );
        // compute cube and add clause
        nFinal = sat_solver_final( pSat, &pFinal );
        uCube = ~(word)0;
        Vec_IntClear( vTemp );
        Vec_IntPush( vTemp, Abc_LitNot(pLits[1]) ); // NOT(iNewLit)
        for ( i = 0; i < nFinal; i++ )
        {
            if ( pFinal[i] == pLits[0] )
                continue;
            Vec_IntPush( vTemp, pFinal[i] );
            iVar = Vec_IntFind( vDivSet, Abc_Lit2Var(pFinal[i]) );   assert( iVar >= 0 );
            uCube &= Abc_LitIsCompl(pFinal[i]) ? s_Truths6[iVar] : ~s_Truths6[iVar];
        }
        uTruth |= uCube;
        status = sat_solver_addclause( pSat, Vec_IntArray(vTemp), Vec_IntArray(vTemp) + Vec_IntSize(vTemp) );
        assert( status );
        nIter++;
    }
    assert( status == l_True );
    // store the counter-example
    Vec_IntForEachEntry( vDivVars, iVar, i )
        Vec_IntAddToEntry( vDivValues, i, sat_solver_var_value(pSat, iVar) );
 
    for ( i = 0; i < Vec_IntSize(vDivValues); i++ )
        Vec_IntAddToEntry( vDivValues, i, 0xC );
/*
    // reduce the counter example
    for ( n = 0; n < 2; n++ )
    {
        Vec_IntClear( vTemp );
        Vec_IntPush( vTemp, Abc_Var2Lit(PivotVar, n) ); // n = 0 => F = 1  (expanding offset against onset)
        for ( i = 0; i < Vec_IntSize(vValues); i++ )
            Vec_IntPush( vTemp, Abc_Var2Lit(i, !((Vec_IntEntry(vValues, i) >> n) & 1)) );
        status = sat_solver_solve( pSat, Vec_IntArray(vTemp), Vec_IntArray(vTemp) + Vec_IntSize(vTemp), nBTLimit, 0, 0, 0 );
        assert( status == l_False );
        // compute cube and add clause
        nFinal = sat_solver_final( pSat, &pFinal );
        for ( i = 0; i < nFinal; i++ )
            if ( Abc_Lit2Var(pFinal[i]) != PivotVar )
                Vec_IntAddToEntry( vValues, Abc_Lit2Var(pFinal[i]), 1 << (n+2) );
    }
*/
    return SBD_SAT_SAT;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Sbd_ManSolve2()

int Sbd_ManSolve2	(	sat_solver *	pSat,
		int	PivotVar,
		int	FreeVar,
		Vec_Int_t *	vDivVars,
		Vec_Int_t *	vDivValues,
		Vec_Int_t *	vTemp,
		Vec_Int_t *	vSop )

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 267 of file sbdWin.c.

{
    int nBTLimit = 0;
    int status, i, iVar, nFinal, * pFinal, pLits[2], nIter = 0;
    assert( FreeVar < sat_solver_nvars(pSat) );
    assert( Vec_IntSize(vDivVars) == Vec_IntSize(vDivValues) );
    pLits[0] = Abc_Var2Lit( PivotVar, 0 ); // F = 1
    pLits[1] = Abc_Var2Lit( FreeVar, 0 );  // iNewLit
    Vec_IntClear( vSop );
    while ( 1 ) 
    {
        // find onset minterm
        status = sat_solver_solve( pSat, pLits, pLits + 2, nBTLimit, 0, 0, 0 );
        if ( status == l_Undef )
            return 0;
        if ( status == l_False )
            return 1;
        assert( status == l_True );
        // remember variable values
        //for ( i = 0; i < Vec_IntSize(vValues); i++ )
        //    Vec_IntWriteEntry( vValues, i, 2*sat_solver_var_value(pSat, i) );
        // collect divisor literals
        Vec_IntClear( vTemp );
        Vec_IntPush( vTemp, Abc_LitNot(pLits[0]) ); // F = 0
        //Vec_IntForEachEntry( vDivSet, iVar, i )
        Vec_IntForEachEntry( vDivVars, iVar, i )
            Vec_IntPush( vTemp, sat_solver_var_literal(pSat, iVar) );
        // check against offset
        status = sat_solver_solve( pSat, Vec_IntArray(vTemp), Vec_IntArray(vTemp) + Vec_IntSize(vTemp), nBTLimit, 0, 0, 0 );
        if ( status == l_Undef )
            return 0;
        if ( status == l_True )
            break;
        assert( status == l_False );
        // compute cube and add clause
        nFinal = sat_solver_final( pSat, &pFinal );
        Vec_IntClear( vTemp );
        Vec_IntPush( vTemp, Abc_LitNot(pLits[1]) ); // NOT(iNewLit)
        for ( i = 0; i < nFinal; i++ )
        {
            if ( pFinal[i] == pLits[0] )
                continue;
            Vec_IntPush( vTemp, pFinal[i] );
            iVar = Vec_IntFind( vDivVars, Abc_Lit2Var(pFinal[i]) );   assert( iVar >= 0 );
            //uCube &= Abc_LitIsCompl(pFinal[i]) ? s_Truths6[iVar] : ~s_Truths6[iVar];
            Vec_IntPush( vSop, Abc_Var2Lit( iVar, !Abc_LitIsCompl(pFinal[i]) ) );
        }
        //uTruth |= uCube;
        Vec_IntPush( vSop, -1 );
        status = sat_solver_addclause( pSat, Vec_IntArray(vTemp), Vec_IntArray(vTemp) + Vec_IntSize(vTemp) );
        assert( status );
        nIter++;
    }
    assert( status == l_True );
    // store the counter-example
    //for ( i = 0; i < Vec_IntSize(vValues); i++ )
    //    Vec_IntAddToEntry( vValues, i, sat_solver_var_value(pSat, i) );
    return 0;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Sbd_ManSolverPrint()

void Sbd_ManSolverPrint

(

Vec_Int_t *

vSop

)

Definition at line 344 of file sbdWin.c.

{
    int v, i, Entry, nVars, pInds[64];
    word Supp = Sbd_ManSolverSupp( vSop, pInds, &nVars );
    char Cube[65] = {'\0'};
    assert( Cube[nVars] == '\0' );
    for ( v = 0; v < nVars; v++ )
        Cube[v] = '-';
    Vec_IntForEachEntry( vSop, Entry, i )
    {
        if ( Entry == -1 )
        {
            printf( "%s\n", Cube );
            for ( v = 0; v < nVars; v++ )
                Cube[v] = '-';
            continue;
        }
        Cube[pInds[Abc_Lit2Var(Entry)]] = '1' - (char)Abc_LitIsCompl(Entry);
    }
    Supp = 0;
}

Here is the call graph for this function:

Sbd_ManSolverSupp()

word Sbd_ManSolverSupp	(	Vec_Int_t *	vSop,
		int *	pInds,
		int *	pnVars )

Definition at line 327 of file sbdWin.c.

{
    word Supp = 0;
    int i, Entry, nVars = 0;
    Vec_IntForEachEntry( vSop, Entry, i )
    {
        if ( Entry == -1 )
            continue;
        assert( Abc_Lit2Var(Entry) < 64 );
        if ( (Supp >> Abc_Lit2Var(Entry)) & 1 )
            continue;
        pInds[Abc_Lit2Var(Entry)] = nVars++;
        Supp |= (word)1 << Abc_Lit2Var(Entry);
    }
    *pnVars = nVars;
    return Supp;
}

Here is the caller graph for this function:

Sbd_ManSolveSelect()

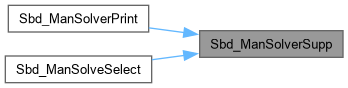
void Sbd_ManSolveSelect	(	Gia_Man_t *	p,
		Vec_Int_t *	vMirrors,
		int	Pivot,
		Vec_Int_t *	vDivVars,
		Vec_Int_t *	vDivValues,
		Vec_Int_t *	vWinObjs,
		Vec_Int_t *	vObj2Var,
		Vec_Int_t *	vTfo,
		Vec_Int_t *	vRoots )

Definition at line 365 of file sbdWin.c.

{
    Vec_Int_t * vSop = Vec_IntAlloc( 100 );
    Vec_Int_t * vTemp = Vec_IntAlloc( 100 );
    sat_solver * pSat = Sbd_ManSatSolver( NULL, p, vMirrors, Pivot, vWinObjs, vObj2Var, vTfo, vRoots, 0 );
    int PivotVar = Vec_IntEntry(vObj2Var, Pivot);
    int FreeVar = Vec_IntSize(vWinObjs) + Vec_IntSize(vTfo) + Vec_IntSize(vRoots);
    int Status = Sbd_ManSolve2( pSat, PivotVar, FreeVar, vDivVars, vDivValues, vTemp, vSop );
    printf( "Pivot = %4d. Divs = %4d.  ", Pivot, Vec_IntSize(vDivVars) );
    if ( Status == 0 )
        printf( "UNSAT.\n" );
    else
    {
        int nVars, pInds[64];
        word Supp = Sbd_ManSolverSupp( vSop, pInds, &nVars );
        //Sbd_ManSolverPrint( vSop );
        printf( "SAT with %d vars and %d cubes.\n", nVars, Vec_IntCountEntry(vSop, -1) );
        Supp = 0;
    }
    Vec_IntFree( vTemp );
    Vec_IntFree( vSop );
    sat_solver_delete( pSat );
}

Here is the call graph for this function: