cecSolveG.c File Reference

#include "cecInt.h"
#include "sat/glucose2/AbcGlucose2.h"

Include dependency graph for cecSolveG.c:

Go to the source code of this file.

Macros
#define	USE_GLUCOSE2
#define	sat_solver   bmcg2_sat_solver
#define	sat_solver_start   bmcg2_sat_solver_start
#define	sat_solver_stop   bmcg2_sat_solver_stop
#define	sat_solver_addclause   bmcg2_sat_solver_addclause
#define	sat_solver_add_and   bmcg2_sat_solver_add_and
#define	sat_solver_add_xor   bmcg2_sat_solver_add_xor
#define	sat_solver_addvar   bmcg2_sat_solver_addvar
#define	sat_solver_reset   bmcg2_sat_solver_reset
#define	sat_solver_set_conflict_budget   bmcg2_sat_solver_set_conflict_budget
#define	sat_solver_conflictnum   bmcg2_sat_solver_conflictnum
#define	sat_solver_solve   bmcg2_sat_solver_solve
#define	sat_solver_read_cex_varvalue   bmcg2_sat_solver_read_cex_varvalue
#define	sat_solver_read_cex   bmcg2_sat_solver_read_cex
#define	sat_solver_jftr   bmcg2_sat_solver_jftr
#define	sat_solver_set_jftr   bmcg2_sat_solver_set_jftr
#define	sat_solver_set_var_fanin_lit   bmcg2_sat_solver_set_var_fanin_lit
#define	sat_solver_start_new_round   bmcg2_sat_solver_start_new_round
#define	sat_solver_mark_cone   bmcg2_sat_solver_mark_cone
#define	sat_solver_varnum   bmcg2_sat_solver_varnum

Functions
int	CecG_ObjSatVarValue (Cec_ManSat_t *p, Gia_Obj_t *pObj)
	FUNCTION DEFINITIONS ///.
void	CecG_AddClausesMux (Cec_ManSat_t *p, Gia_Obj_t *pNode)
void	CecG_AddClausesSuper (Cec_ManSat_t *p, Gia_Obj_t *pNode, Vec_Ptr_t *vSuper)
void	CecG_CollectSuper_rec (Gia_Obj_t *pObj, Vec_Ptr_t *vSuper, int fFirst, int fUseMuxes, int fUseSuper)
void	CecG_CollectSuper (Gia_Obj_t *pObj, int fUseMuxes, int fUseSuper, Vec_Ptr_t *vSuper)
void	CecG_ObjAddToFrontier (Cec_ManSat_t *p, Gia_Obj_t *pObj, Vec_Ptr_t *vFrontier)
void	CecG_CnfNodeAddToSolver (Cec_ManSat_t *p, Gia_Obj_t *pObj)
void	CecG_ManSatSolverRecycle (Cec_ManSat_t *p)
int	CecG_ManSatCheckNode (Cec_ManSat_t *p, Gia_Obj_t *pObj)
void	CecG_ManSatSolve (Cec_ManPat_t *pPat, Gia_Man_t *pAig, Cec_ParSat_t *pPars, int f0Proved)

Macro Definition Documentation

sat_solver

#define sat_solver   bmcg2_sat_solver

Definition at line 30 of file cecSolveG.c.

sat_solver_add_and

#define sat_solver_add_and   bmcg2_sat_solver_add_and

Definition at line 34 of file cecSolveG.c.

sat_solver_add_xor

#define sat_solver_add_xor   bmcg2_sat_solver_add_xor

Definition at line 35 of file cecSolveG.c.

sat_solver_addclause

#define sat_solver_addclause   bmcg2_sat_solver_addclause

Definition at line 33 of file cecSolveG.c.

sat_solver_addvar

#define sat_solver_addvar   bmcg2_sat_solver_addvar

Definition at line 36 of file cecSolveG.c.

sat_solver_conflictnum

#define sat_solver_conflictnum   bmcg2_sat_solver_conflictnum

Definition at line 39 of file cecSolveG.c.

sat_solver_jftr

#define sat_solver_jftr   bmcg2_sat_solver_jftr

Definition at line 43 of file cecSolveG.c.

sat_solver_mark_cone

#define sat_solver_mark_cone   bmcg2_sat_solver_mark_cone

Definition at line 47 of file cecSolveG.c.

sat_solver_read_cex

#define sat_solver_read_cex   bmcg2_sat_solver_read_cex

Definition at line 42 of file cecSolveG.c.

sat_solver_read_cex_varvalue

#define sat_solver_read_cex_varvalue   bmcg2_sat_solver_read_cex_varvalue

Definition at line 41 of file cecSolveG.c.

sat_solver_reset

#define sat_solver_reset   bmcg2_sat_solver_reset

Definition at line 37 of file cecSolveG.c.

sat_solver_set_conflict_budget

#define sat_solver_set_conflict_budget   bmcg2_sat_solver_set_conflict_budget

Definition at line 38 of file cecSolveG.c.

sat_solver_set_jftr

#define sat_solver_set_jftr   bmcg2_sat_solver_set_jftr

Definition at line 44 of file cecSolveG.c.

sat_solver_set_var_fanin_lit

#define sat_solver_set_var_fanin_lit   bmcg2_sat_solver_set_var_fanin_lit

Definition at line 45 of file cecSolveG.c.

sat_solver_solve

#define sat_solver_solve   bmcg2_sat_solver_solve

Definition at line 40 of file cecSolveG.c.

sat_solver_start

#define sat_solver_start   bmcg2_sat_solver_start

Definition at line 31 of file cecSolveG.c.

sat_solver_start_new_round

#define sat_solver_start_new_round   bmcg2_sat_solver_start_new_round

Definition at line 46 of file cecSolveG.c.

sat_solver_stop

#define sat_solver_stop   bmcg2_sat_solver_stop

Definition at line 32 of file cecSolveG.c.

sat_solver_varnum

#define sat_solver_varnum   bmcg2_sat_solver_varnum

Definition at line 49 of file cecSolveG.c.

USE_GLUCOSE2

#define USE_GLUCOSE2

CFile****************************************************************

FileName [cecSolve.c]

SystemName [ABC: Logic synthesis and verification system.]

PackageName [Combinational equivalence checking.]

Synopsis [Performs one round of SAT solving.]

Author [Alan Mishchenko]

Affiliation [UC Berkeley]

Date [Ver. 1.0. Started - June 20, 2005.]

Revision [

Id

cecSolve.c,v 1.00 2005/06/20 00:00:00 alanmi Exp

]

Definition at line 24 of file cecSolveG.c.

Function Documentation

CecG_AddClausesMux()

void CecG_AddClausesMux	(	Cec_ManSat_t *	p,
		Gia_Obj_t *	pNode )

Function*************************************************************

Synopsis [Addes clauses to the solver.]

Description []

SideEffects []

SeeAlso []

Definition at line 117 of file cecSolveG.c.

{
    Gia_Obj_t * pNodeI, * pNodeT, * pNodeE;
    int pLits[4], RetValue, VarF, VarI, VarT, VarE, fCompT, fCompE;
 
    assert( !Gia_IsComplement( pNode ) );
    assert( Gia_ObjIsMuxType( pNode ) );
    // get nodes (I = if, T = then, E = else)
    pNodeI = Gia_ObjRecognizeMux( pNode, &pNodeT, &pNodeE );
    // get the variable numbers
    VarF = CecG_ObjSatNum(p,pNode);
    VarI = CecG_ObjSatNum(p,pNodeI);
    VarT = CecG_ObjSatNum(p,Gia_Regular(pNodeT));
    VarE = CecG_ObjSatNum(p,Gia_Regular(pNodeE));
    // get the complementation flags
    fCompT = Gia_IsComplement(pNodeT);
    fCompE = Gia_IsComplement(pNodeE);
 
    // f = ITE(i, t, e)
 
    // i' + t' + f
    // i' + t  + f'
    // i  + e' + f
    // i  + e  + f'
 
    // create four clauses
    pLits[0] = toLitCond(VarI, 1);
    pLits[1] = toLitCond(VarT, 1^fCompT);
    pLits[2] = toLitCond(VarF, 0);
    if ( p->pPars->fPolarFlip )
    {
        if ( pNodeI->fPhase )               pLits[0] = lit_neg( pLits[0] );
        if ( Gia_Regular(pNodeT)->fPhase )  pLits[1] = lit_neg( pLits[1] );
        if ( pNode->fPhase )                pLits[2] = lit_neg( pLits[2] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, 3 );
    assert( RetValue );
    pLits[0] = toLitCond(VarI, 1);
    pLits[1] = toLitCond(VarT, 0^fCompT);
    pLits[2] = toLitCond(VarF, 1);
    if ( p->pPars->fPolarFlip )
    {
        if ( pNodeI->fPhase )               pLits[0] = lit_neg( pLits[0] );
        if ( Gia_Regular(pNodeT)->fPhase )  pLits[1] = lit_neg( pLits[1] );
        if ( pNode->fPhase )                pLits[2] = lit_neg( pLits[2] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, 3 );
    assert( RetValue );
    pLits[0] = toLitCond(VarI, 0);
    pLits[1] = toLitCond(VarE, 1^fCompE);
    pLits[2] = toLitCond(VarF, 0);
    if ( p->pPars->fPolarFlip )
    {
        if ( pNodeI->fPhase )               pLits[0] = lit_neg( pLits[0] );
        if ( Gia_Regular(pNodeE)->fPhase )  pLits[1] = lit_neg( pLits[1] );
        if ( pNode->fPhase )                pLits[2] = lit_neg( pLits[2] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, 3 );
    assert( RetValue );
    pLits[0] = toLitCond(VarI, 0);
    pLits[1] = toLitCond(VarE, 0^fCompE);
    pLits[2] = toLitCond(VarF, 1);
    if ( p->pPars->fPolarFlip )
    {
        if ( pNodeI->fPhase )               pLits[0] = lit_neg( pLits[0] );
        if ( Gia_Regular(pNodeE)->fPhase )  pLits[1] = lit_neg( pLits[1] );
        if ( pNode->fPhase )                pLits[2] = lit_neg( pLits[2] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, 3 );
    assert( RetValue );
 
    // two additional clauses
    // t' & e' -> f'
    // t  & e  -> f 
 
    // t  + e   + f'
    // t' + e'  + f 
 
    if ( VarT == VarE )
    {
//        assert( fCompT == !fCompE );
        return;
    }
 
    pLits[0] = toLitCond(VarT, 0^fCompT);
    pLits[1] = toLitCond(VarE, 0^fCompE);
    pLits[2] = toLitCond(VarF, 1);
    if ( p->pPars->fPolarFlip )
    {
        if ( Gia_Regular(pNodeT)->fPhase )  pLits[0] = lit_neg( pLits[0] );
        if ( Gia_Regular(pNodeE)->fPhase )  pLits[1] = lit_neg( pLits[1] );
        if ( pNode->fPhase )                pLits[2] = lit_neg( pLits[2] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, 3 );
    assert( RetValue );
    pLits[0] = toLitCond(VarT, 1^fCompT);
    pLits[1] = toLitCond(VarE, 1^fCompE);
    pLits[2] = toLitCond(VarF, 0);
    if ( p->pPars->fPolarFlip )
    {
        if ( Gia_Regular(pNodeT)->fPhase )  pLits[0] = lit_neg( pLits[0] );
        if ( Gia_Regular(pNodeE)->fPhase )  pLits[1] = lit_neg( pLits[1] );
        if ( pNode->fPhase )                pLits[2] = lit_neg( pLits[2] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, 3 );
    assert( RetValue );
}

Here is the call graph for this function:

Here is the caller graph for this function:

CecG_AddClausesSuper()

void CecG_AddClausesSuper	(	Cec_ManSat_t *	p,
		Gia_Obj_t *	pNode,
		Vec_Ptr_t *	vSuper )

Function*************************************************************

Synopsis [Addes clauses to the solver.]

Description []

SideEffects []

SeeAlso []

Definition at line 236 of file cecSolveG.c.

{
    Gia_Obj_t * pFanin;
    int * pLits, nLits, RetValue, i;
    assert( !Gia_IsComplement(pNode) );
    assert( Gia_ObjIsAnd( pNode ) );
    // create storage for literals
    nLits = Vec_PtrSize(vSuper) + 1;
    pLits = ABC_ALLOC( int, nLits );
    // suppose AND-gate is A & B = C
    // add !A => !C   or   A + !C
    Vec_PtrForEachEntry( Gia_Obj_t *, vSuper, pFanin, i )
    {
        pLits[0] = toLitCond(CecG_ObjSatNum(p,Gia_Regular(pFanin)), Gia_IsComplement(pFanin));
        pLits[1] = toLitCond(CecG_ObjSatNum(p,pNode), 1);
        if ( p->pPars->fPolarFlip )
        {
            if ( Gia_Regular(pFanin)->fPhase )  pLits[0] = lit_neg( pLits[0] );
            if ( pNode->fPhase )                pLits[1] = lit_neg( pLits[1] );
        }
        RetValue = sat_solver_addclause( p->pSat, pLits, 2 );
        assert( RetValue );
    }
    // add A & B => C   or   !A + !B + C
    Vec_PtrForEachEntry( Gia_Obj_t *, vSuper, pFanin, i )
    {
        pLits[i] = toLitCond(CecG_ObjSatNum(p,Gia_Regular(pFanin)), !Gia_IsComplement(pFanin));
        if ( p->pPars->fPolarFlip )
        {
            if ( Gia_Regular(pFanin)->fPhase )  pLits[i] = lit_neg( pLits[i] );
        }
    }
    pLits[nLits-1] = toLitCond(CecG_ObjSatNum(p,pNode), 0);
    if ( p->pPars->fPolarFlip )
    {
        if ( pNode->fPhase )  pLits[nLits-1] = lit_neg( pLits[nLits-1] );
    }
    RetValue = sat_solver_addclause( p->pSat, pLits, nLits );
    assert( RetValue );
    ABC_FREE( pLits );
}

Here is the caller graph for this function:

CecG_CnfNodeAddToSolver()

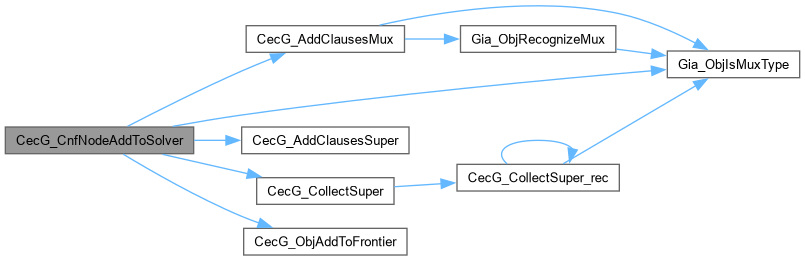
void CecG_CnfNodeAddToSolver	(	Cec_ManSat_t *	p,
		Gia_Obj_t *	pObj )

Function*************************************************************

Synopsis [Updates the solver clause database.]

Description []

SideEffects []

SeeAlso []

Definition at line 364 of file cecSolveG.c.

{ 
    Vec_Ptr_t * vFrontier;
    Gia_Obj_t * pNode, * pFanin;
    int i, k, fUseMuxes = 0 == p->pPars->SolverType;
    // quit if CNF is ready
    if ( CecG_ObjSatNum(p,pObj) )
        return;
    if ( Gia_ObjIsCi(pObj) )
    {
        Vec_PtrPush( p->vUsedNodes, pObj );
        CecG_ObjSetSatNum( p, pObj, sat_solver_addvar( p->pSat ) );
        return;
    }
    assert( Gia_ObjIsAnd(pObj) );
 
    // start the frontier
    vFrontier = Vec_PtrAlloc( 100 );
    CecG_ObjAddToFrontier( p, pObj, vFrontier );
    // explore nodes in the frontier
    Vec_PtrForEachEntry( Gia_Obj_t *, vFrontier, pNode, i )
    {
        // create the supergate
        assert( CecG_ObjSatNum(p,pNode) );
        if ( fUseMuxes && Gia_ObjIsMuxType(pNode) )
        {
            Vec_PtrClear( p->vFanins );
            Vec_PtrPushUnique( p->vFanins, Gia_ObjFanin0( Gia_ObjFanin0(pNode) ) );
            Vec_PtrPushUnique( p->vFanins, Gia_ObjFanin0( Gia_ObjFanin1(pNode) ) );
            Vec_PtrPushUnique( p->vFanins, Gia_ObjFanin1( Gia_ObjFanin0(pNode) ) );
            Vec_PtrPushUnique( p->vFanins, Gia_ObjFanin1( Gia_ObjFanin1(pNode) ) );
            Vec_PtrForEachEntry( Gia_Obj_t *, p->vFanins, pFanin, k )
                CecG_ObjAddToFrontier( p, Gia_Regular(pFanin), vFrontier );
            CecG_AddClausesMux( p, pNode );
        }
        else
        {
            CecG_CollectSuper( pNode, fUseMuxes, 0 == p->pPars->SolverType, p->vFanins );
            Vec_PtrForEachEntry( Gia_Obj_t *, p->vFanins, pFanin, k )
                CecG_ObjAddToFrontier( p, Gia_Regular(pFanin), vFrontier );
            
            if( p->pPars->SolverType < 2 )
                CecG_AddClausesSuper( p, pNode, p->vFanins );
        }
        assert( Vec_PtrSize(p->vFanins) > 1 );
    }
    if( p->pPars->SolverType )
        Vec_PtrForEachEntry( Gia_Obj_t *, vFrontier, pNode, i ){
            int var = CecG_ObjSatNum( p, pNode );
            int Lit0 = Abc_Var2Lit( CecG_ObjSatNum( p, Gia_ObjFanin0(pNode) ), Gia_ObjFaninC0(pNode) );
            int Lit1 = Abc_Var2Lit( CecG_ObjSatNum( p, Gia_ObjFanin1(pNode) ), Gia_ObjFaninC1(pNode) );
            assert(Gia_ObjIsAnd(pNode));
            if ( (Lit0 > Lit1) ^ Gia_ObjIsXor(pNode) )
                 Lit1 ^= Lit0, Lit0 ^= Lit1, Lit1 ^= Lit0;
            sat_solver_set_var_fanin_lit( p->pSat, var, Lit0, Lit1 );
        }
    Vec_PtrFree( vFrontier );
}

Here is the call graph for this function:

Here is the caller graph for this function:

CecG_CollectSuper()

void CecG_CollectSuper	(	Gia_Obj_t *	pObj,
		int	fUseMuxes,
		int	fUseSuper,
		Vec_Ptr_t *	vSuper )

Function*************************************************************

Synopsis [Collects the supergate.]

Description []

SideEffects []

SeeAlso []

Definition at line 320 of file cecSolveG.c.

{
    assert( !Gia_IsComplement(pObj) );
    assert( !Gia_ObjIsCi(pObj) );
    Vec_PtrClear( vSuper );
    CecG_CollectSuper_rec( pObj, vSuper, 1, fUseMuxes, fUseSuper );
}

Here is the call graph for this function:

Here is the caller graph for this function:

CecG_CollectSuper_rec()

void CecG_CollectSuper_rec	(	Gia_Obj_t *	pObj,
		Vec_Ptr_t *	vSuper,
		int	fFirst,
		int	fUseMuxes,
		int	fUseSuper )

Function*************************************************************

Synopsis [Collects the supergate.]

Description []

SideEffects []

SeeAlso []

Definition at line 289 of file cecSolveG.c.

{
    // if the new node is complemented or a PI, another gate begins
    if ( Gia_IsComplement(pObj) || Gia_ObjIsCi(pObj) || 
         (!fFirst && Gia_ObjValue(pObj) > 1) || 
         (fUseMuxes && Gia_ObjIsMuxType(pObj)) )
    {
        Vec_PtrPushUnique( vSuper, pObj );
        return;
    }
    if( !fUseSuper ){
        Vec_PtrPushUnique( vSuper, Gia_ObjChild0(pObj) );
        Vec_PtrPushUnique( vSuper, Gia_ObjChild1(pObj) );
        return ;
    }
    // go through the branches
    CecG_CollectSuper_rec( Gia_ObjChild0(pObj), vSuper, 0, fUseMuxes, fUseSuper );
    CecG_CollectSuper_rec( Gia_ObjChild1(pObj), vSuper, 0, fUseMuxes, fUseSuper );
}

Here is the call graph for this function:

Here is the caller graph for this function:

CecG_ManSatCheckNode()

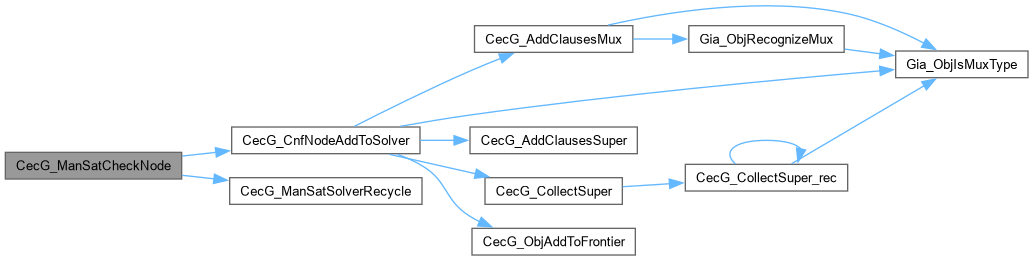
int CecG_ManSatCheckNode	(	Cec_ManSat_t *	p,
		Gia_Obj_t *	pObj )

Function*************************************************************

Synopsis [Runs equivalence test for the two nodes.]

Description []

SideEffects []

SeeAlso []

Definition at line 479 of file cecSolveG.c.

{
    Gia_Obj_t * pObjR = Gia_Regular(pObj);
    int nBTLimit = p->pPars->nBTLimit;
    int Lit, RetValue, nConflicts;
    abctime clk = Abc_Clock();
 
    if ( pObj == Gia_ManConst0(p->pAig) )
        return 1;
    if ( pObj == Gia_ManConst1(p->pAig) )
    {
        assert( 0 );
        return 0;
    }
 
    p->nCallsSince++;  // experiment with this!!!
    p->nSatTotal++;
    
    // check if SAT solver needs recycling
    if ( p->pSat == NULL || 
        (p->pPars->nSatVarMax && 
         sat_solver_varnum(p->pSat) > p->pPars->nSatVarMax && 
         p->nCallsSince > p->pPars->nCallsRecycle) )
        CecG_ManSatSolverRecycle( p );
 
    // if the nodes do not have SAT variables, allocate them
    CecG_CnfNodeAddToSolver( p, pObjR );
 
    if( p->pPars->SolverType ){
        sat_solver_start_new_round( p->pSat );
        sat_solver_mark_cone( p->pSat, CecG_ObjSatNum(p, pObjR) );
    }
 
    // propage unit clauses // minisat only
    //if ( p->pSat->qtail != p->pSat->qhead )
    //{
    //    status = sat_solver_simplify(p->pSat);
    //    assert( status != 0 );
    //    assert( p->pSat->qtail == p->pSat->qhead );
    //}
 
    // solve under assumptions
    // A = 1; B = 0     OR     A = 1; B = 1 
    Lit = toLitCond( CecG_ObjSatNum(p,pObjR), Gia_IsComplement(pObj) );
    if ( p->pPars->fPolarFlip )
    {
        if ( pObjR->fPhase )  Lit = lit_neg( Lit );
    }
    nConflicts = sat_solver_conflictnum(p->pSat);
 
    sat_solver_set_conflict_budget( p->pSat, nBTLimit );
    RetValue = sat_solver_solve( p->pSat, &Lit, 1 );
    //RetValue = sat_solver_solve( p->pSat, &Lit, &Lit + 1, 
    //    (ABC_INT64_T)nBTLimit, (ABC_INT64_T)0, (ABC_INT64_T)0, (ABC_INT64_T)0 );
    if ( RetValue == l_False )
    {
p->timeSatUnsat += Abc_Clock() - clk;
        Lit = lit_neg( Lit );
        RetValue = sat_solver_addclause( p->pSat, &Lit, 1 );
        assert( RetValue );
        p->nSatUnsat++;
        p->nConfUnsat += sat_solver_conflictnum(p->pSat) - nConflicts;       
//Abc_Print( 1, "UNSAT after %d conflicts\n", sat_solver_conflictnum(p->pSat) - nConflicts );
        return 1;
    }
    else if ( RetValue == l_True )
    {
p->timeSatSat += Abc_Clock() - clk;
        p->nSatSat++;
        p->nConfSat += sat_solver_conflictnum(p->pSat) - nConflicts;
//Abc_Print( 1, "SAT after %d conflicts\n", sat_solver_conflictnum(p->pSat) - nConflicts );
        return 0;
    }
    else // if ( RetValue == l_Undef )
    {
p->timeSatUndec += Abc_Clock() - clk;
        p->nSatUndec++;
        p->nConfUndec += sat_solver_conflictnum(p->pSat) - nConflicts;
//Abc_Print( 1, "UNDEC after %d conflicts\n", sat_solver_conflictnum(p->pSat) - nConflicts );
        return -1;
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

CecG_ManSatSolve()

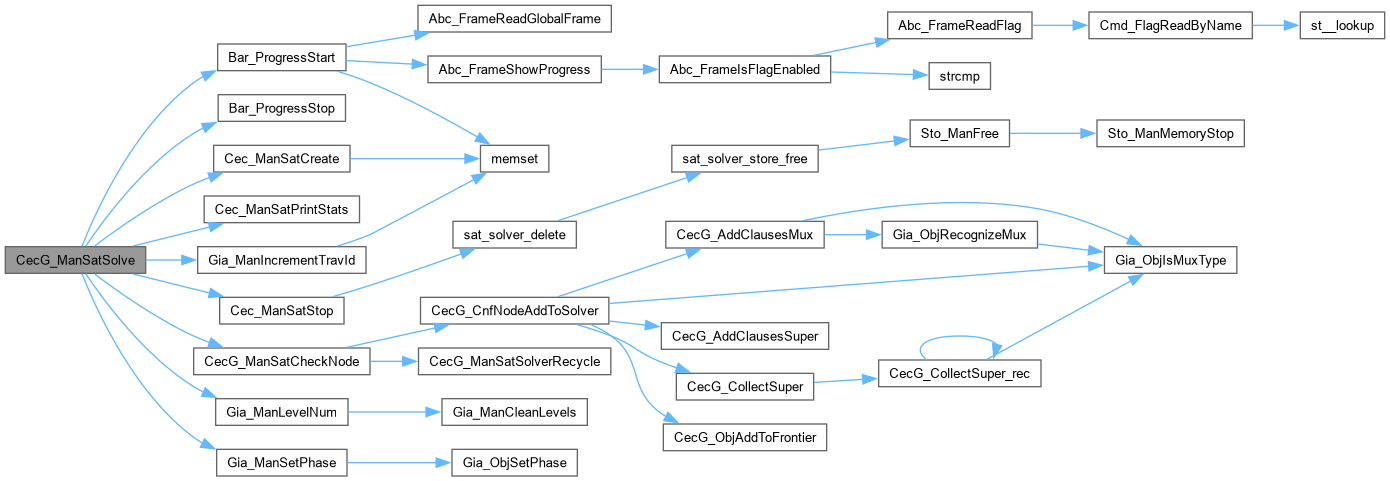
void CecG_ManSatSolve	(	Cec_ManPat_t *	pPat,
		Gia_Man_t *	pAig,
		Cec_ParSat_t *	pPars,
		int	f0Proved )

Definition at line 562 of file cecSolveG.c.

{
    Bar_Progress_t * pProgress = NULL;
    Cec_ManSat_t * p;
    Gia_Obj_t * pObj;
    int i, status;
    abctime clk = Abc_Clock(), clk2;
    Vec_PtrFreeP( &pAig->vSeqModelVec );
    if( pPars->SolverType )
        pPars->fPolarFlip = 0;
    // reset the manager
    if ( pPat )
    {
        pPat->iStart = Vec_StrSize(pPat->vStorage);
        pPat->nPats = 0;
        pPat->nPatLits = 0;
        pPat->nPatLitsMin = 0;
    } 
    Gia_ManSetPhase( pAig );
    Gia_ManLevelNum( pAig );
    Gia_ManIncrementTravId( pAig );
    p = Cec_ManSatCreate( pAig, pPars );
    pProgress = Bar_ProgressStart( stdout, Gia_ManPoNum(pAig) );
    Gia_ManForEachCo( pAig, pObj, i )
    {
        if ( Gia_ObjIsConst0(Gia_ObjFanin0(pObj)) )
        {
            status = !Gia_ObjFaninC0(pObj);
            pObj->fMark0 = (status == 0);
            pObj->fMark1 = (status == 1);
            continue;
        }
        Bar_ProgressUpdate( pProgress, i, "SAT..." );
clk2 = Abc_Clock();
        status = CecG_ManSatCheckNode( p, Gia_ObjChild0(pObj) );
        pObj->fMark0 = (status == 0);
        pObj->fMark1 = (status == 1);
 
        if ( f0Proved && status == 1 )
            Gia_ManPatchCoDriver( pAig, i, 0 );
/*
        if ( status == -1 )
        {
            Gia_Man_t * pTemp = Gia_ManDupDfsCone( pAig, pObj );
            Gia_AigerWrite( pTemp, "gia_hard.aig", 0, 0, 0 );
            Gia_ManStop( pTemp );
            Abc_Print( 1, "Dumping hard cone into file \"%s\".\n", "gia_hard.aig" );
        }
*/
        if ( status != 0 )
            continue;
        // save the pattern
        //if ( pPat )
        //{
        //    abctime clk3 = Abc_Clock();
        //    Cec_ManPatSavePattern( pPat, p, pObj );
        //    pPat->timeTotalSave += Abc_Clock() - clk3;
        //}
        // quit if one of them is solved
        if ( pPars->fCheckMiter )
            break;
    }
    p->timeTotal = Abc_Clock() - clk;
    printf("Recycles %d\n", p->nRecycles);
    Bar_ProgressStop( pProgress );
    if ( pPars->fVerbose )
        Cec_ManSatPrintStats( p );
    if( p->pSat )
        sat_solver_stop( p->pSat );
    p->pSat = NULL;
    Cec_ManSatStop( p );
}

Here is the call graph for this function:

Here is the caller graph for this function:

CecG_ManSatSolverRecycle()

void CecG_ManSatSolverRecycle

(

Cec_ManSat_t *

p

)

Function*************************************************************

Synopsis [Recycles the SAT solver.]

Description []

SideEffects []

SeeAlso []

Definition at line 435 of file cecSolveG.c.

{
    int Lit;
    if ( p->pSat )
    {
        Gia_Obj_t * pObj;
        int i;
        Vec_PtrForEachEntry( Gia_Obj_t *, p->vUsedNodes, pObj, i )
            CecG_ObjSetSatNum( p, pObj, 0 );
        Vec_PtrClear( p->vUsedNodes );
//        memset( p->pSatVars, 0, sizeof(int) * Gia_ManObjNumMax(p->pAigTotal) );
        sat_solver_stop( p->pSat );
    }
    p->pSat = (struct sat_solver_t*)sat_solver_start();
    assert( 0 <= p->pPars->SolverType && p->pPars->SolverType <= 2 );
    sat_solver_set_jftr( p->pSat, p->pPars->SolverType );
    //sat_solver_setnvars( p->pSat, 1000 ); // minisat only
    //p->pSat->factors = ABC_CALLOC( double, p->pSat->cap );
    // var 0 is not used
    // var 1 is reserved for const0 node - add the clause
 
//    p->nSatVars = 0;
    CecG_ObjSetSatNum( p, Gia_ManConst0(p->pAig), sat_solver_addvar( p->pSat ) );
    Lit = toLitCond( CecG_ObjSatNum( p, Gia_ManConst0(p->pAig) ), 1 );
    sat_solver_addclause( p->pSat, &Lit, 1 );
//    if ( p->pPars->fPolarFlip ) // no need to normalize const0 node (bug fix by SS on 9/17/2012)
//        Lit = lit_neg( Lit );
 
    p->nRecycles++;
    p->nCallsSince = 0;
}

Here is the caller graph for this function:

CecG_ObjAddToFrontier()

void CecG_ObjAddToFrontier	(	Cec_ManSat_t *	p,
		Gia_Obj_t *	pObj,
		Vec_Ptr_t *	vFrontier )

Function*************************************************************

Synopsis [Updates the solver clause database.]

Description []

SideEffects []

SeeAlso []

Definition at line 339 of file cecSolveG.c.

{
    assert( !Gia_IsComplement(pObj) );
    if ( CecG_ObjSatNum(p,pObj) )
        return;
    assert( CecG_ObjSatNum(p,pObj) == 0 );
    if ( Gia_ObjIsConst0(pObj) )
        return;
    Vec_PtrPush( p->vUsedNodes, pObj );
    CecG_ObjSetSatNum( p, pObj, sat_solver_addvar( p->pSat ) );
    if ( Gia_ObjIsAnd(pObj) )
        Vec_PtrPush( vFrontier, pObj );
}

Here is the caller graph for this function:

CecG_ObjSatVarValue()

int CecG_ObjSatVarValue	(	Cec_ManSat_t *	p,
		Gia_Obj_t *	pObj )

FUNCTION DEFINITIONS ///.

Function*************************************************************

Synopsis [Returns value of the SAT variable.]

Description []

SideEffects []

SeeAlso []

Definition at line 101 of file cecSolveG.c.

{ 
    return sat_solver_read_cex_varvalue( p->pSat, CecG_ObjSatNum(p, pObj) );
}